Исследование точности и стабильности технологического процесса обработки кольца подшипника, страница 3

Если , то технологический процесс по точности соответствует требованиям чертежа.

Если , то точность процесса не соответствует требованиям чертежа. Для принятия решения об изменении технологического процесса обработки детали с целью повышение его точности вычисляется вероятность брака. Для этого находится диапазон размеров, которые выходят за поле допуска, и вычисляется вероятность попадания размеров в этот диапазон (Х_н…Х_в):

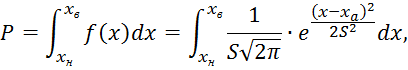
где Х_в – верхнее значение диапазона; Х_н – нижнее значение диапазона.

Пример

Далее выполним точности и стабильности технологического процесса шлифования  детали типа наружного кольца подшипника на бортикошлифовальном станке-автомате.

Для выполнения такого исследования взята выборка последовательно обработанных 60 деталей. По результатам измерений наружного диаметра кольца подшипника сформирован интервальный ряд. Этот ряд имеет К=8 интервалов с шагом h=0,03мм. Значения среди интервалов x_i – от 19,815 мм до 19,895мм. Частоты интервалов (числа деталей, попавших в интервал) n_i следуют в порядке возрастания номера интервала 1,3,5,11,12,5,2,1. В приложении А. Приведены исследования точности и стабильности точения . Значения середин интервалов x_i заданы дискретным аргументом от 19,815 с шагом 0,01, а также приведены частоты n_i, расчет среднего арифметического x_a и среднего квадратичного отклонения S.

После этого строится гистограмма частот n_i и по виду ее делается вывод о предполагаемом теоретическом распределении, хорошо описывающем наблюдаемое, т.е. статистическое.

В приложении А приведена гистограмма частот n_i , расположенных по оси абсцисс над соответствующим значением X_i. Для этого строится график n_i(X_i) при помощи прямоугольников (bar). Такая возможность имеется в «Mathcad».

Вид гистограммы n_i(X_i) напоминает колокообразную кривую плотности нормального распределения для описания исследуемого размера.

Полезно еще рассчитать теоретические частоты nt_i по формулам нормального распределения и, построив график nt_i(X_i), сравнить его с n_i(X_i), что более наглядно позволит увидеть отличительные особенности нормального распределения и статистического (наблюдаемого). Расчет теоретических частот выполнен по формулам, приведенным в теоретических положениях, и в приложении А. На гистограмме частот nt_i(X_i). Еще раз убеждаемся, что различие между гистограммой и графиком теоретических частот невелико, что позволяет высказать гипотезу о приемлемости нормального распределения для описания статистического.

Окончательный вывод о приемлемости теоретического распределения для описания статистического сделаем по критериям согласия Колмогорова и Пирсона.

В приложении А рассматривается расчет критерия Колмогорова. В результате расчета получено, что расчетное значение критерия  меньше табличного λ_1-р. Поэтому гипотезу принимаем.

Выполним еще проверку гипотезы и по более строгому критерию согласия Пирсона. Анализ теоретических nt_i и наблюдаемых n_i частот показывает, что первые две и последние две частоты в этих рядах меньше 5. Поэтому первые две объединяем с третьей частотой, а последние две – с седьмой частотой. Это выполнено на рис.  В результате получается не 9 частот , а только 5. Ряды этих частот – в столбцах n_i и nt_i. Расчетное значение критерия Пирсона χ вычисляется по формуле, приведенной в теоретических положениях, а табличное – для числа степеней свободы f=             и уровня значимости Р=       (из Приложения 5[]), т.к. , то и по критерию Пирсона гипотеза о приемлемости нормального распределения для описания статистического принимается.

Таким образом, технологический процесс точения роликов полностью устойчивый.

Теперь необходимо сравнить исследуемый процесс точения с требованием чертежа по точности. Сравнение выполняется расчетом коэффициента точности Km.Получаем Km=      , т.е. Km>1.Это говорит о том, что процесс не соответствует по точности рассеивания размеров при точении превосходит допуск.

Полезно для принятия решения по данному техпроцессу знать ожидаемый процент брака. Для этого сначала определяем диапазон размеров, которые выходят за поле допуска, сравнением максимальных и минимальных размеров по чертежу A_max, A_min, с A1_max, A1_min которые формируются техпроцессом. Устанавливаем, что ожидаемый диапазон размеров вне поля допуска -    …. . Вычисленная вероятность Р попадания в этот диапазон равна   , т.е. ожидаемый брак составит     % от деталей, протачиваемых на автомате.