Розрахунок асинхронного двигуна (номінальна напруга 220/380 В (фазна/лінійна), частота 50 Гц)

2.3 Розрахунок асинхронного двигуна

Двигун який використовується в даному електроприводі являється асинхронним коротко замкнутим. Для розрахунку трифазного асинхронного двигуна приймаємо такі дані:

номінальна напруга 220/380 В (фазна/лінійна) при частоті ;

номінальне ковзання ;

потужність на валу ;

число пар полюсів ;

перевантажена здатність з обертового моменту ;

схема з’єднання обмоток статора – зірка (рис 2.3);

ККД ;

коефіцієнт потужності ;

кратність пускового струму .

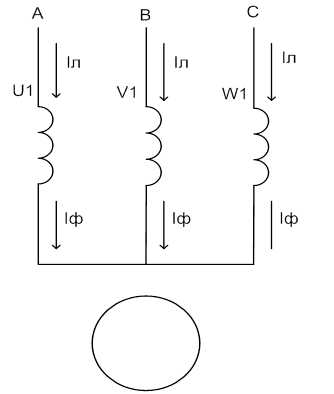
Рисунок 2.3 - Електрична схема з’єднання обмоток статора – зірка

При з’єднанні обмоток статора зіркою:

                                                     (2.1)

де - відповідно лінійна і фазна напруга обмотки статора. Тому лінійна напруга мережі:

                                               (2.2)

Синхронна частота обертання поля статора

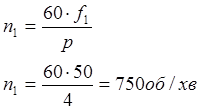                                       (2.3)

Номінальна частота обертання ротора:

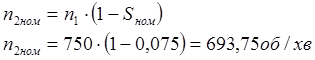                    (2.4)

Щоб визначити критичну частоту обертання ротора

                                                 (2.5)

необхідно знати критичне ковзання двигуна . Це таке ковзання , при якому обертаючий момент  досягає максимального значення.

Для визначення  використовуємо відому формулу Клосса.

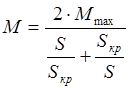                                                  (2.6)

і номінальний режим роботи двигуна, при якому номінальному значенню ковзання відповідає номінальне значення обертаючого моменту.

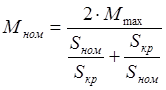                                           (2.7)

Зважаючи на те, що перевантажна здатність з обертаючого моменту 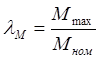, з попередньої формули маємо

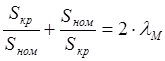                                             (2.8)

звідки отримуємо квадратне рівняння:

                                   (2.9)

розв’язання якого дає вираз та значення критичного ковзання: 

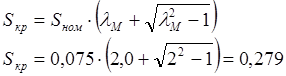                            (2.10)

Таким чином, критична частота обертання ротора

Номінальна потужність, споживана двигуном із мережі:

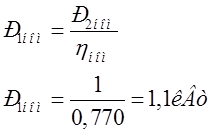                                       (2.11)

Сума всіх втрат у двигуні

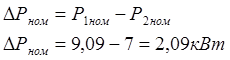                                  (2.12)

При напрузі мережі  фази обмотки статора з’єднуються зіркою. При цьому лінійний і фазний струми однакові:

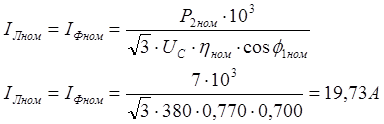         (2.13)

Пускові струми

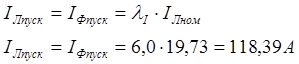                           (2.14)

Номінальний і максимальний обертаючі моменти

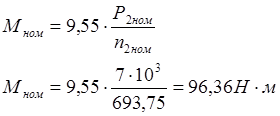                             (2.15)

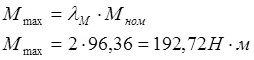                                  (2.16)

Тепер, задаючись значеннями від  до , необхідно визначити значення обертаючого моменту за формулою Клосса. При цьому зауважимо, що на частині залежності, яка відповідає стійким режимам роботи двигуна , достатньо мати чотири точки при

            

На ділянці залежності  з нестійкими режимами роботи двигуна () можна задатися такими значеннями ковзання . Результати розрахунку зведено до табл.2.1.

Пусковий момент двигуна визначається при  і дорівнює , тоді кратність цього моменту

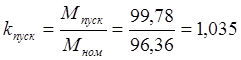                                 (2.17)

Таблиця 2.1 - Дані розрахунку залежності

	0		0,1		0,3	0,4	0,6	0,8	1,0
	0	96,62	122,44	192,72	192,24	180,83	147,39	119,85	99,78

За даними таблиці 2.1. на рис.2.4 зображено залежність  .

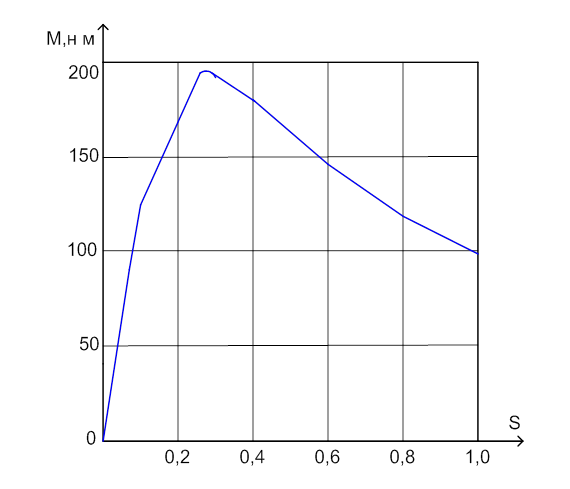
Рисунок 2.4 - Графік залежності

Природну механічну характеристику  при  отримуємо шляхом окремих розрахунків частоти обертання і обертаючого моменту на основі виразів, у які входить один аргумент – ковзання :

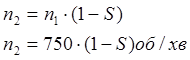;                                         (2.18)

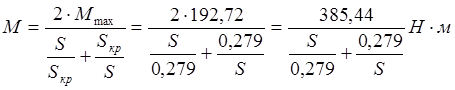          (2.19)

Тепер, щоб отримати природну механічну характеристику, достатньо задати ряд значень  від  до  і виконати розрахунки за наведеними формулами. Значення ковзання  для механічної характеристики вибирається таким же чином, як і для залежності . У тому числі, завжди треба робити розрахунок для значень ковзання  і .

Результати розрахунку зведено до табл.2.2, де ще додано значення , яке визначається далі ( важливо для однієї з штучних характеристик).

За даними табл.2.2 на рис. 2.5 зображено природну механічну характеристику  при .

Щоб отримати штучну механічну характеристику при зниженні напруги живильної мережі на %, тобто , скористаємося таким ж формулами, що і в попередньому випадку для природної механічної характеристики. Але при цьому треба враховувати те, що максимальний обертаючий момент змінюється у залежності від цієї напруги таким чином

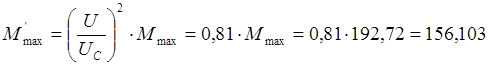               (2.20)

Тобто штучну механічну характеристику при таких умовах визначаємо для тих же значень ковзання  і частоти обертання , розраховуючи обертаючий момент за формулою

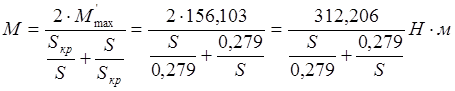                          (2.21)

(як відомо, значення  не залежить від величини напруги живлення).

Результати розрахунків зведено до табл.. 2.2.

За даними табл. 2.2 на рис. 2.5 зображено штучну механічну характеристику  при .

Ця і попередня механічні характеристики отримані при умові, що фази обмотки ротора мають тільки свій активний опір, тобто немає ніяких додаткових опорів .

Таблиця 2.2 – Дані розрахунку механічних характеристики асинхронного двигуна

	0	0,075	0,1	0,2	0,279	0,4	0,558	0,6	0,8	1,0
	750	694	675	600	541	450	332	300	150	0
при  ,	0	96,63	122	185	192,7	181	154	147	120	100
при  ,	0	78,26	99	148	156	147	125	120	97	81
при  ,	0	50,88	67	122	154	183	192,7	192	181	164

Щоб отримати штучну механічну характеристику при введенні у фази обмотки ротора регулювальних реостатів з опорами , скористаємося такими ж формулами, що і у випадку для природної механічної характеристики. Але при цьому треба врахувати те, що тепер змінюється критичне ковзання, яке взагалі визначається за відомою формулою .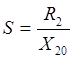

Тому, при додаванні до  ще регулювального реостата з опором  та збереженні індуктивного опору фази обмотки статора , складемо пропорцію і отримаємо нове значення критичного ковзання для штучної механічної характеристики, що розглядається, тобто

                   (2.22)

Максимальний обертаючий момент  не залежить від  та  і зберігається таким, що і для природної механічної характеристики (його тепер буде отримано при новому значенні критичного ковзання ). Ця штучна механічна характеристика розраховується при напрузі живлення .

Таким чином, штучну механічну характеристику при визначених умовах  отримуємо для тих же значень ковзання  і частоти обертання , що і в попередніх випадках, розраховуючи обертаючий момент за модифікованою формулою

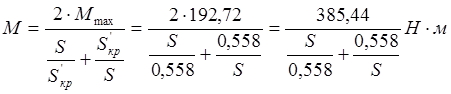                   (2.23)     

Результати розрахунків зведені до табл.2.2.

За даними табл.2.2 на рис. 2.5 зображено штучну механічну характеристику  при  і .

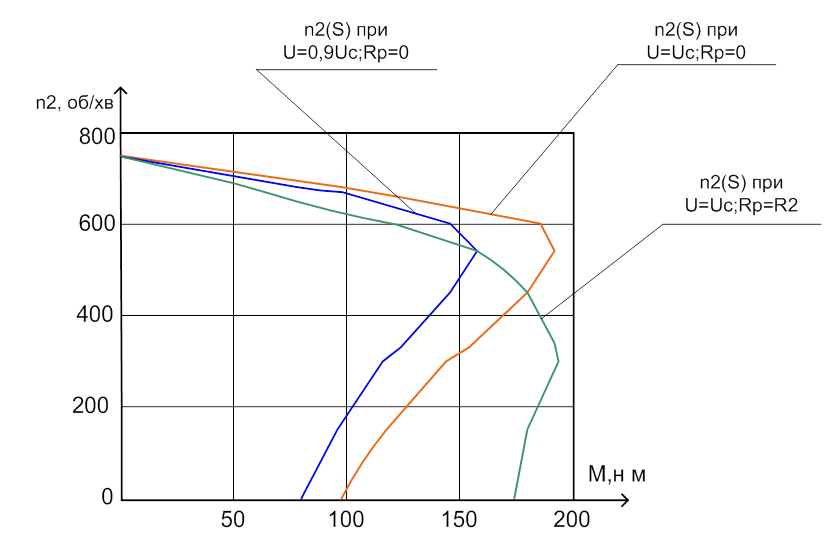
Рисунок 2.5 - Графіки залежностей механічних характеристик