kh = 1 - коэффициент, учитывающий изменение высоты поперечного сечения деревянных элементов (по таблице 2.7 [1]);
С учетом соответствующих коэффициентов
fv.о.d=![]()
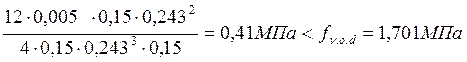 .
.
Проверка выполняется, следовательно, сечение принято верно.
Проверка на прочность:
Должно удовлетворяться следующее условие:
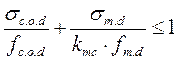 .
.
Расчётное сжимающее напряжение:
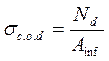 ;
; 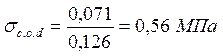 ;
;
где Asup = 0,15 × 0,837 = 0,126 м2 - максимальная площадь сечения;
Nd = 0,071 МН - продольная сила в данном сечении.
Коэффициент, учитывающий увеличение напряжений при изгибе:
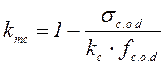 .
.
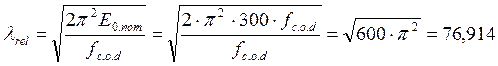 .
.
Гибкость сечения:
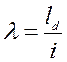 ,
,
ld - расчетная длина, равная в данном случае длине полурамы,
ld = 20,336 м (п.7.3.3.2 [1]).
Радиус инерции сечения:
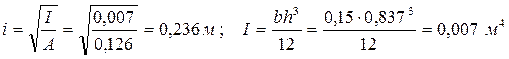 ;
;
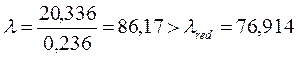 ,
следовательно,
,
следовательно, 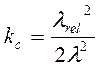 ;
;
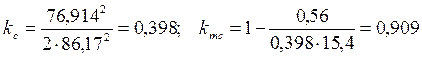 .
.
Расчётное напряжение изгиба:
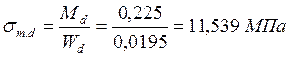 .
.
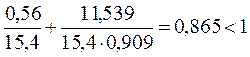 -
проверка выполняется, следовательно, оставляем принятое сечение.
-
проверка выполняется, следовательно, оставляем принятое сечение.
Проверка на устойчивость плоской формы деформирования сжато-изгибаемых элементов:
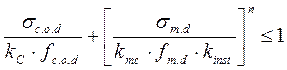
kinst - коэффициент устойчивости изгибаемого элемента:
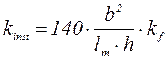
Покрытие из плит шириной 1,1 м раскрепляет верхнюю
растянутую кромку рамы, для этого устраиваем скатные раскосы через 2 плиты. Расчетная длина при этом будет равна длинам
внешних подкрепленных кромок ригеля и стойки: ![]() = lm=2,1 м.
= lm=2,1 м.
Гибкость 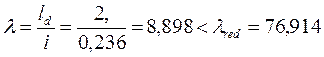 ,следовательно,
,следовательно,
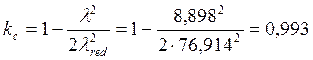 ;
; 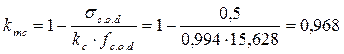 .
.
kf - коэффициент, зависящий от формы эпюры изгибающих моментов на участке lm = 2,1 м (табл. 7.4 [1]).
![]() ;
;
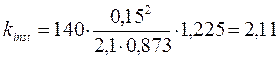 .
.
n= 1- показатель степени, учитывающий раскрепление растянутой кромки из плоскости, для элементов, имеющих такое раскрепление (п. 5.5 [1]).
Расчётное сжимающее напряжение:
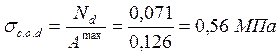 .
.
Расчётное напряжение от изгиба:
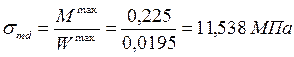 .
.
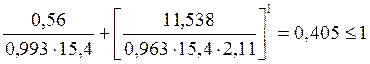 -
условие выполняется.
-
условие выполняется.
Коньковый узел решается с помощью стальных креплений. Расчёт производится на действие максимальных:
- продольная сила Fd(N)=Q∙sin10º+N∙cos10º=5,54·sin10º+26,31·cos10º=26,872кН= =0,0269 МН;
- поперечная сила Vd(Q)=Q∙cos10º+N∙sin10º=5,54·cos10º +26,31·sin22º = 10 кН = = 0,01 МН.
Проверка торцевого сечения на смятие под углом a = 10°
scm.a. d £ ks1×ks 2×fc.a. d
Расчетное сопротивление смятию древесины под углом к волокнам:
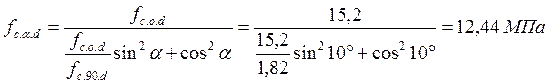 ,
,
fc.о.d=![]() ;
;
fc.90.d=![]() (при kx = 1, kmod=1,2, ks = 0,9, kh = 0,89, kd = 1,05).
(при kx = 1, kmod=1,2, ks = 0,9, kh = 0,89, kd = 1,05).
Расчётное напряжение смятия под углом к волокнам древесины:
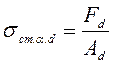 ,
,
Ad– площадь опорной площадки торца полрамы, определяемая из условия смятия:
Ad = N/![]() = 0,0269 / 12,44 = 0,0022 м2;
= 0,0269 / 12,44 = 0,0022 м2;
Ad= b·hd, следовательно, hd = Ad / b= 0,0022 / 0,15 = 0,015 м, примем hd = 0,156 м.
тогда Ad = 0,15×0,156 = 0,0234 м2.
lsk = 0,061 м;
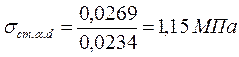 .
.
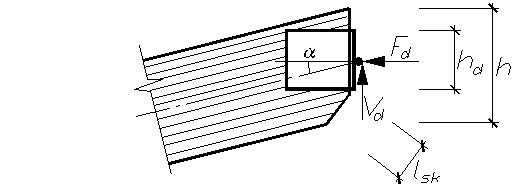
Рис. 2.7 Схема конькового узла полурамы
Коэффициенты, учитывающие неравномерность распределения напряжений под плитой башмака:
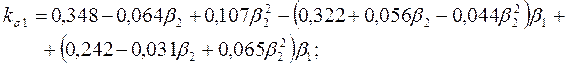
![]() , где
, где 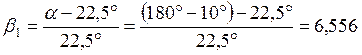 ;
;
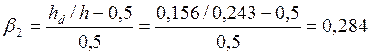 ;
;
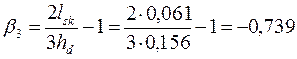 ;
;
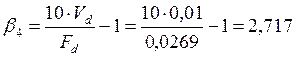 .
.
ks1 = -0,283;
ks2= -0,735.
1,15 МПа ![]() 0,283 × 0,735 × 12,44 = 2,59 МПа - условие на смятие выполняется.
0,283 × 0,735 × 12,44 = 2,59 МПа - условие на смятие выполняется.
Металлические пластины крепятся к торцам полурам при помощи болтов диаметром 12 мм. Фасонки выполняются из стальных листов толщиной 10мм, размерами 156х150 мм.
Минимальные расстояния между болтами определяются по таблице 4.6. [1]. Вдоль волокон между осями болтов и до торца элемента не менее чем 7·d=7·12=84 мм; поперек волокон между осями болтов не менее чем 3,5·d=3,5·12=42 мм; поперек волокон до кромки элемента не менее чем 3·d=3·12=36 мм.
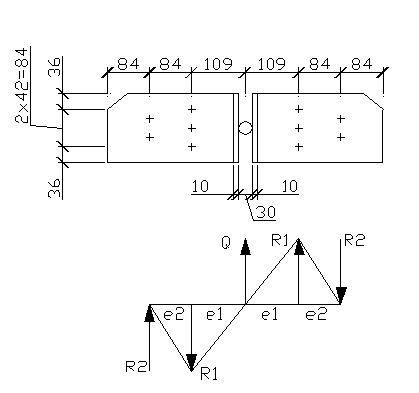
Рис. 2.8 Схема накладок конькового узла полурамы
Усилия, действующие на болты:
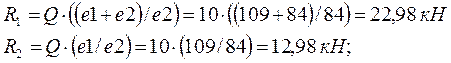
Расчётная несущая способность соединения:
Rd = R1d.min × nn × ns
Расчётную несущую способность одного среза нагеля в симметричном соединении с обоими внешними элементами из стали следует принимать равной меньшему значению из полученных по формулам:
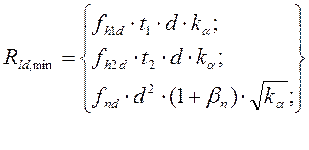 , где t2=0,15м – толщина среднего элемента;
, где t2=0,15м – толщина среднего элемента;
d=0,012 м – диаметр болта;
bnmax=0,6236 (т. 4.3 [1]);
ka = 0,95 – коэффициент, учитывающий угол между усилием и направлением волокон древесины (табл.. 4.4 [1]);
![]() (табл. 4.2 [1]);
(табл. 4.2 [1]);
![]() – расчётное значение
сопротивления изгибу болта (т. 4.3 [1]),
– расчётное значение
сопротивления изгибу болта (т. 4.3 [1]),
![]() ;
;
![]() .
.
Принимаем минимальное значение несущей способности одного
среза болта диаметром 12 мм ![]() .
.
Находим требуемое количество болтов при ns=2 – количество швов в соединении для одного нагеля:
- по внутренним осям 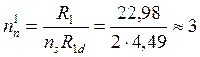 болтов,
болтов,
- по крайним осям 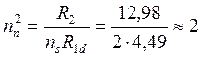 болтов.
болтов.
Принимаем nn =5 болтов Æ12 мм.
Расчётная несущая способность соединения:
Rd=4,49·5=22,45 кН > Vd=10 кН.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.