Введение в теорию расчета статически неопределимых систем, страница 4

зоваться  внутренние  усилия  в  лишних  связях  или  узловые  перемещения стержневой конструкции.

В  зависимости  от  природы  используемых  основных  неизвестных различают  следующие классические  методы решения частной  задачи  или методы расчета статически неопределимых стержневых конструкций:

-   метод  сил  – в качестве  основных  неизвестных  используются  внутренние усилия в лишних связях стержневой конструкции;

-   метод перемещений - в качестве основных неизвестных используются узловые перемещения стержневой конструкции;

-   смешанный  метод  -  в  качестве  основных  неизвестных  одновременно используются величины первого и второго вида.

Суть  расчета  статически  неопределимых  стержневых  конструкций названными  методами                                      состоит  в  следующем.  Расчет  заданной  конструк- ции  заменяется  расчетом  некоторой  более  простой  эквивалентной  конст- рукцией.  Такая  конструкция  называется  основной  системой,  образование которой  для  каждого  метода  производится  по-разному.                         Затем,  исходя  из особенностей   деформирования   заданной   конструкции   в   определенных местах, получают дополнительные уравнения. Такие уравнения называются каноническими уравнениями соответствующего метода. Решение кано- нических  уравнений  позволяет  определить  основные  неизвестные.  После этого определяют требуемые внутренние усилия и перемещения заданной конструкции.

7.4.Сутьметода сил

Поясним суть метода сил на примере один раз статически неопреде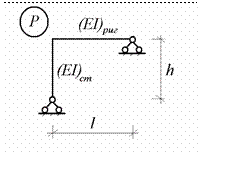лимой рамы (рис. 7.4)

Рис. 7.4

Для рамы считаются известными геометрические размеры, материал и  геометрические  характеристики  поперечных  сечений  конструкционных

элементов. На раму действует некоторая произвольная нагрузка. Под дей- ствием нагрузки рама деформируется, и в ней возникают внутренние уси- лия  –  изгибающие  моменты,  поперечные  и  продольные  силы.  Исходное состояние рамы называется заданной системой.

Лишней  связью  в  рассматриваемой  раме  является  любой  опорный стержень. Для определенности примем за лишнюю связь горизонтальный опорный стержень на правой опоре рамы. Для образования основной сис- темы метода сил отбросим лишнюю связь и заменим ее действие реакцией

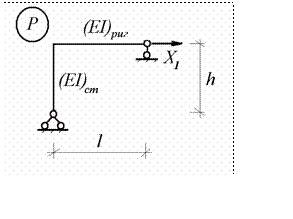удаленной связи (7.5)

Рис.7.5

Реакция удаленной лишней связи является основным неизвестным метода сил. Приложение основного неизвестного в качестве дополнитель- ного внешнего воздействия позволяет устранить различие внутренних уси- лий двух систем или восстановить статическую эквивалентность.

От действия основного неизвестного и заданной нагрузки в статиче- ски  определимой  системе  возникает  горизонтальное  перемещение  правой опоры, которое отсутствует в заданной системе. Для устранения различий перемещений  двух  систем  или  восстановления  кинематической  эквива- лентности вводится условие обращения в ноль указанного перемещения

D (X , P) = 0 .                                                                          (7.6)

1  1

Статически  определимая  рама  (рис.7.5),  для  которой  соблюдаются требования  статической  и  кинематической  эквивалентности,  и  является основной  системой  метода  сил  рассматриваемой  рамы.  Дальнейшее  оп- ределение искомых внутренних усилий производится в основной системе, которая полностью эквивалентна заданной раме.

Считая основную систему, как и заданную раму, линейно деформируемыми,  условие  (7.6)  разворачивается  в  дополнительное  уравнение  относительно основного неизвестного  X1

d11 X1  + D1P= 0 .                                                   (7.7)

Уравнение (7.7) называется каноническим уравнением метода сил.

Входящие в это уравнение величины

d11    и

D1P

являются перемеще-

ниями  в  основной  системе  по  направлению  удаленной  связи  от  действия