Введение в теорию расчета статически неопределимых систем, страница 2

7.1.3. Универсальная формула

Полученные  формулы  (7.1)  –  (7.4)  позволяют  определять  степень статической  неопределимости  для  любых  плоских  стержневых  конструк- ций. Формула (7.1) справедлива для конструкций, не имеющих замкнутых контуров. Формула (7.2) применима для конструкций, состоящих из одних замкнутых контуров. Формула (7.3) распространяется на конструкции, со- стоящие из замкнутых контуров с врезанными в них шарнирами. И, нако- нец, формула (7.4) позволяет определить степень статической неопредели- мости  для  стержневых  конструкций,  имеющих  участки,  как  содержащие замкнутые контуры, так и не содержащие их.

Однако  существует  формула,  позволяющая  единообразно  опреде- лять  степень  статической  неопределимости  во  всех  рассмотренных  выше случаях. Рассмотрим ее получение на частном примере рамы, показанной

на рис. 7.3.а

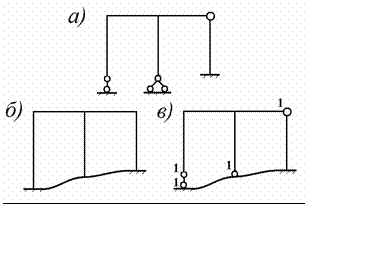
Рис. 7.3

Искусственно  преобразуем  заданную  раму  в  конструкцию,  состоя- щую  из  одних  замкнутых  контуров.  Для  этого  заменим  шарнирный  узел жестким,  шарнирные  опоры  защемляющими  и  «замкнём»  раму  диском

«земля» (рис. 7.3.б). Получим конструкцию, состоящую из двух замкнутых контуров.

Осуществим обратный переход от полученной конструкции к исход- ной  раме.  Для  этого  врежем  в  искусственную  конструкцию  5  удаленных шарниров (рис. 7.3.в). Тогда по формуле (7.3) получим

Л= 3 × 2 - 4 = 2 .

Проверим полученный результат по формуле (7.1). Для конструкции, показанной на рис. 7.3.а

W= -2 , и, следовательно, получим тоже значение степени статической неопределимости

Таким образом, формула

Л= 2 .

Л= 3K - Ш

(7.5)

является универсальной и может применяться для подсчета степени статической неопределимости любой плоской стержневой конструкции.

Величина К, входящая в формулу (7.5),  определяет число замкнутых контуров искусственной конструкции. Для её получения необходимо в за- данной конструкции заменить все шарнирные соединения (внутренние узлы и опорные закрепления) жесткими, а также «замкнуть» ее диском «земля».

Величина  Ш,  входящая  в  формулу  (7.5),   определяет  число  шарниров, которые нужно ввести в искусственную конструкцию, чтобы получить из нее заданную конструкцию. Подсчет числа вводимых шарниров ведется с учетом их кратности.

7.1.4. Составляющие степени статической неопределимости

Формулы (7.4) и (7.5) позволяют определить для произвольной пло- ской стержневой конструкции степень полной статической неопределимо- сти. В общем случае эта величина складывается из двух составляющих

Л = Л1  + Л 2 ,

где

Л1 - число внешних лишних связей, определяющих степень внешней

статической  неопределимости  конструкции,

Л2      -  число  внутренних

лишних связей, определяющих степень внутренней статической неопре-

делимости конструкции.

Число внешних лишних связей определяется по формуле

Л1  = C0  - 3 - Cзам,

где  C0

-  общее  число  опорных  стержней  конструкции;

Cзам

-  число

опорных  стержней,  заменяющих  недостающие  внутренние  связи  в  конструкции отделённой от опорных закреплений.

Число внутренних лишних связей определяется по формуле

Л2  = Л- Л1 .

В зависимости от значений, принимаемых

Л1   и

Л 2 , принято разли-

чать  следующие  разновидности  статически  неопределимых  стержневых конструкций:

-   Л1  ¹ 0  и

Л 2  = 0

- внешне статически неопределимые стержне-

выеконструкции;

-   Л1  = 0  и

Л 2  ¹ 0

- внутренне статически неопределимые стерж-

невые конструкции;

-   Л1  ¹ 0  и

Л 2  ¹ 0

- статически неопределимые стержневые кон-