Динамический расчет систем с конечным числом степеней свободы на вибрационную нагрузку

МО                                                             РБ

Полоцкий   государственный    университет

Кафедра  строительной

                            механики

Расчётно-графическая работа №1

по теме:

 «Динамический расчет систем с конечным числом степеней свободы на вибрационную

нагрузку »

    Выполнил:                                                Матвейчев А.В.

                                                             гр. 06ПГС-5                                                                                     

   Проверил:                                                 Турищев Л.С.                           

Новополоцк

                                         2009

Вариант задания - 8

§1. Расчет на свободные колебания.

1) Описание физических свойств материала.

Материал балки сталь Ст.3.

Расчетное сопротивление R = 210МПа, модуль упругости Е = 2·10⁵МПа.

Отношение .

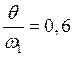2) Образование расчетной схемы.

Рис.1. Расчетная схема

l = 3м;

m = 2700кг; H = 2,7кН.

ε₁=1;  ε₂=0,8; ε₃=0,5

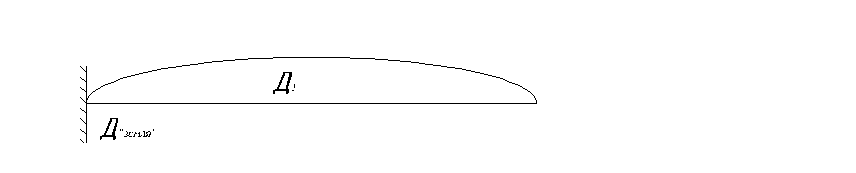1.1. Изображение расчетной схемы безмассовой стержневой системы в виде кинематической цепи.

Рис.2. Изображение расчетной схемы в виде кинематической цепи

1.2. Подсчет числа степеней свободы безмассовой стержневой системы.

Д = 1, У = 0, Ш = 0, С = 0, Соп = 3.

W = 3Д + 2У – 2Ш – С – Соп = 3 – 3 = 0.

Вывод: система может быть геометрически неизменяемой и статически определимой.

1.3. Анализ геометрической структуры.

Диск Д₁ крепится к земле при помощи 3-х стержней, не пересекающихся в одной точке и не параллельных между собой, и образует с ним единый неподвижный диск.

Вывод о статических и кинематических свойствах расчетной схемы безмассовой стержневой системы.

Вывод: система геометрически неизменяема и статически определима.

§2. Определение собственных частот и собственных форм свободных колебаний системы.

2.1.Определение числа степеней свобода деформируемой

стержневой системы.

1) Изображение отклоненного положения системы и независимых перемещений присоединенных к ней масс без учета допущений.

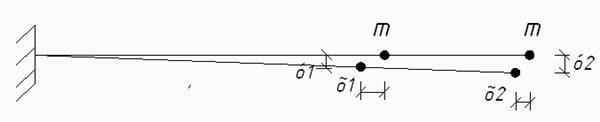
2) Определение полного числа степеней свободы.

3) Изображение отклоненного положения системы и независимых перемещений присоединенных к ней масс с учетом допущений.

4) Определение неполного числа степеней свободы.

2.2.Образуем основную систему обратного метода.

2.3. Составление в обратной форме дифференциальных уравнений движения с учетом допущений.

,

.

2.4. Решаем систему дифференциальных уравнений свободных колебаний.

,

,

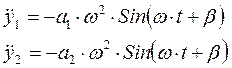
Подставляем данные выражения в систему уравнений

,

.

Данное выражение представляет собой систему однородных линейных алгебраических уравнений.

Такая система может иметь 2 решения:

1)  когда а₁=0 либо а₂=0

2)  когда имеется бесконечное множество решений

Первый вариант нас не удовлетворяет, так как в данном случае система будет находиться в состоянии покоя, следовательно, будем решать систему исходя из того, что она имеет бесконечное множество решений. Для этого составляем определитель системы, который должен равняться нулю.

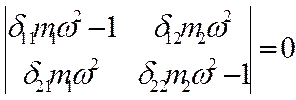
2.5. Для определения  рассмотрим основную систему обратного метода в двух единичных состояниях и построим единичные эпюры.

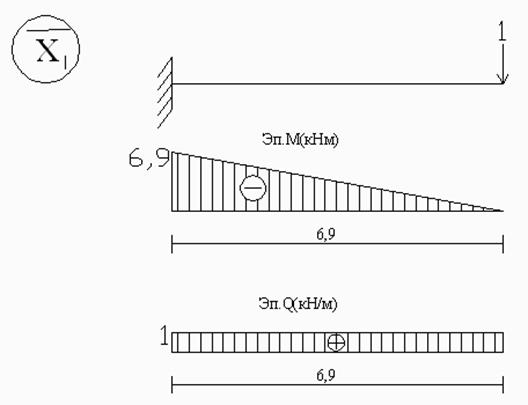
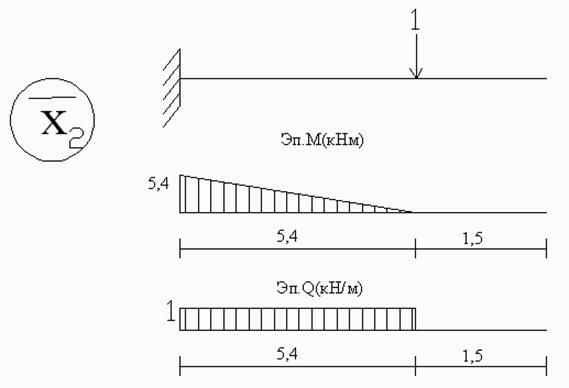
Теперь определяем :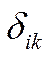

    

2.6. Подставляем найденные значения и  масс в определитель. Преобразуем его, раскроем и получим преобразованное частотное уравнение свободных колебаний.

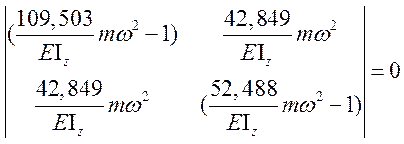
Умножим каждый член на 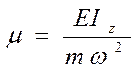  и получим:

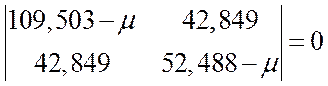
Раскрываем определитель:

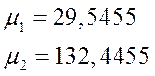
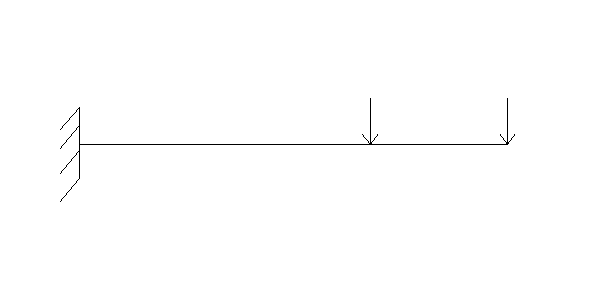
2.7. Подберём нужный номер двутавра исходя из условия статической прочности на изгиб.

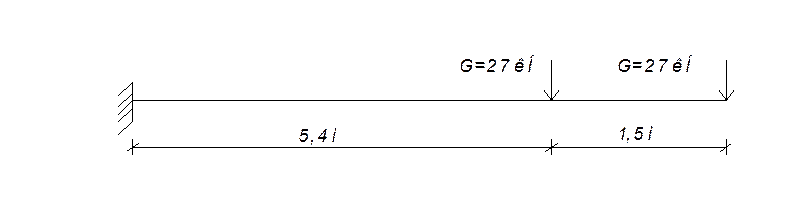
Рис.3.

кН

2) Вычисление опорных реакций.

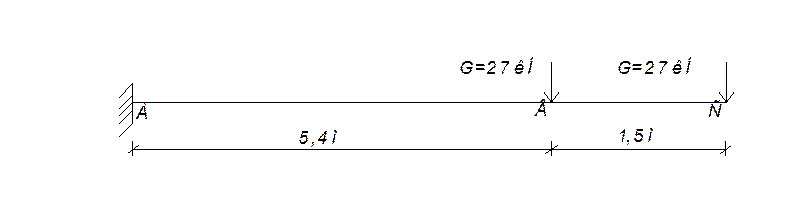3) Получение аналитических выражений, описывающих изменение внутренних усилий по участкам.

Участок СВ (0 ≤ х ≤ 1,5м):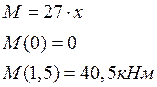          

кН,

кН.

Участок ВА (0 ≤ х ≤ 5,4м):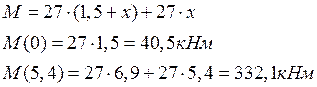          

кН,

кН.

4) Построение эпюр внутренних усилий.

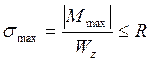,                                                 (1)

Откуда,

.

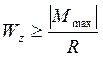R = 210МПа, M_max = 40,5кН·м.

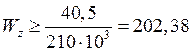см³.

По сортаменту выбираем поперечное сечение: двутавр №20а, W_z = 203cм³,

I_z = 2030cм⁴.

Находим круговые частоты:

так как 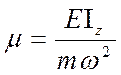, то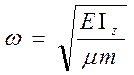

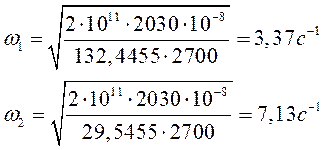
      2.8. Строим спектр собственных круговых частот.

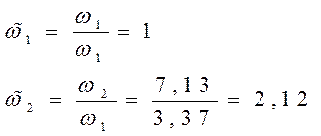
                2.9. Строим собственные формы свободных колебаний

I форма с           

Пусть , тогда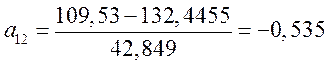 

II форма с         

Пусть , тогда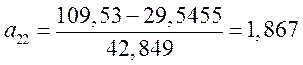 

I Форма

     

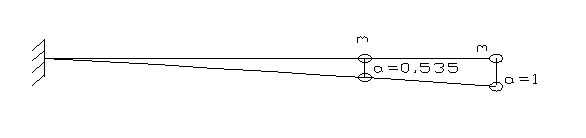
IIФорма

      

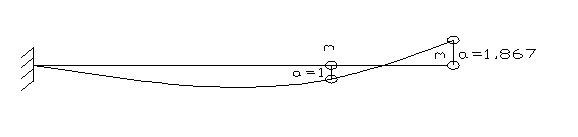
2.10. Проверим свойство ортогональности :    

Проверка выполняется.

  2.11. Определение нормирующих множителей для I и II форм свободных колебаний.

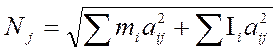
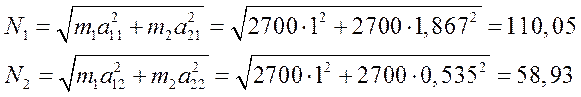
Определим величину ортонормированных амплитуд для I и II форм свободных колебаний.

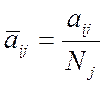
I форма:    

                       

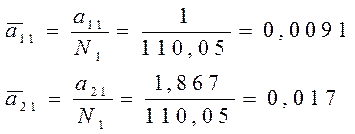
II форма

                                                

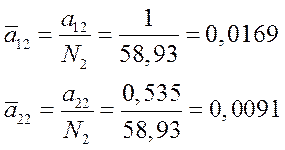
Проверим правильность вычисления ортонормированных амплитуд:

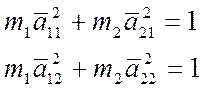
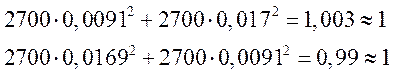
§3 Динамический расчёт системы на действие вибрационной нагрузки.

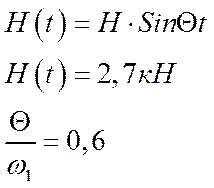
3.1.Составляем систему дифференциальных уравнений вынужденных колебаний в обратной форме.

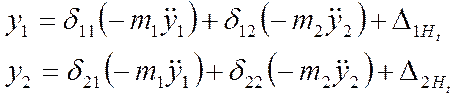
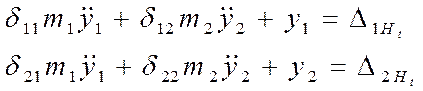
3.2. Решаем систему дифференциальных уравнений:

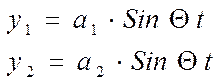
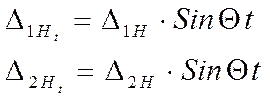
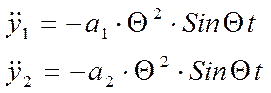
Подставляем данные выражения в систему уравнений и получаем :

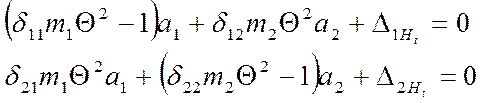
3.3. Преобразуем систему амплитудных уравнений вынужденных колебаний в систему уравнений амплитудных значений сил инерции

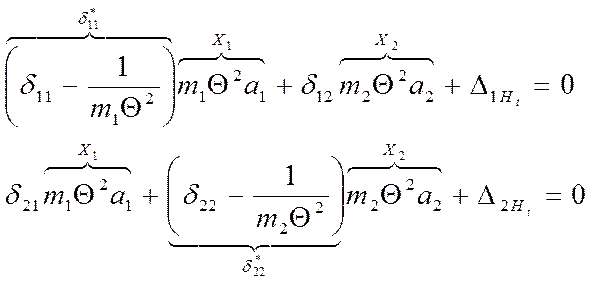
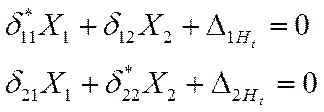
3.4.Найдём значение коэффициентов

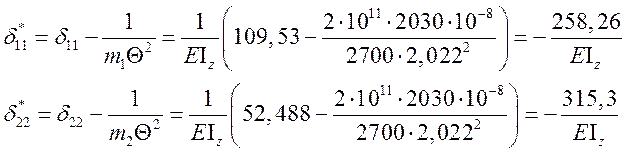
3.4. Определим значения , для этого основную систему обратного метода рассмотрим на действие амплитудного значения возмущающей нагрузки и построим эпюру М_н

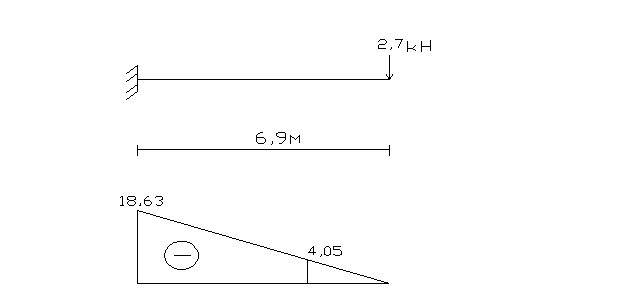
Определим

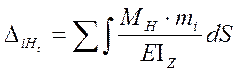
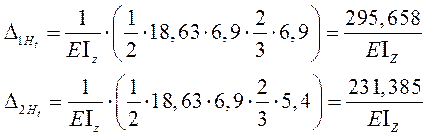
Решаем систему уравнений:

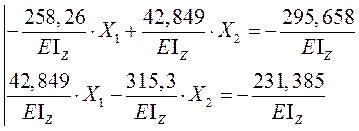
Умножим оба уравнения на (-EIz) и получим:

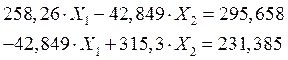
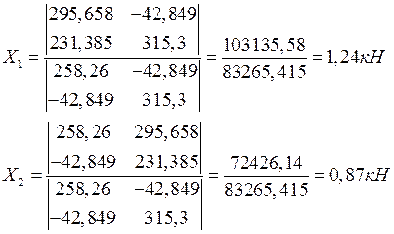
Строим эпюры  и :

           

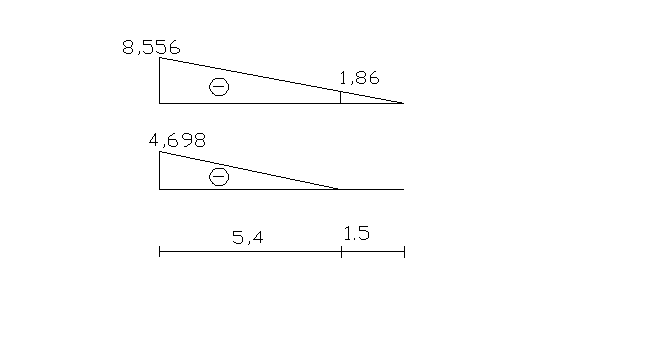
Построим эпюру динамических усилий от действия сил инерции:

 

Проверка выполнения условий предельных состояний для колеблющейся стержневой системы.

      1)Проверка выполнения условий первой группы предельных состояний.

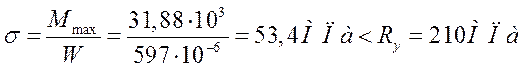
      2)Проверка выполнения условий второй  группы предельных состояний.

        l/f=(5/48)×Мl²/EЈ≤1/200

        l/f=(5/48) ×(5,02×10³×5²)/(2×10¹¹×27440×0.01⁴)=0,0023≤1/200=0,005

      3)Заключение о возможности эксплуатации колеблющейся стержневой системы.

      Данная колеблющаяся стержневая система пригодна к эксплуатации, т.к. проверки по предельным группам состояний выполняются.