Расчет плоской рамы на устойчивость

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

Учреждение образования

«ПОЛОЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Кафедра механики

РАСЧЁТНО-ПРОЕКТИРОВОЧНАЯ РАБОТА № 2

по строительной механике

«РАСЧЕТ ПЛОСКОЙ РАМЫ НА УСТОЙЧИВОСТЬ»

Выполнила                                                       студентка группы 06-ПГС-5

Матвейчев А.В.

Проверил                                                                                   Турищев Л.С.

Новополоцк  2009

ВАРИАНТ № 6

Для заданной плоской статически неопределимой рамы определить низшую нагрузку, используя метод перемещений.

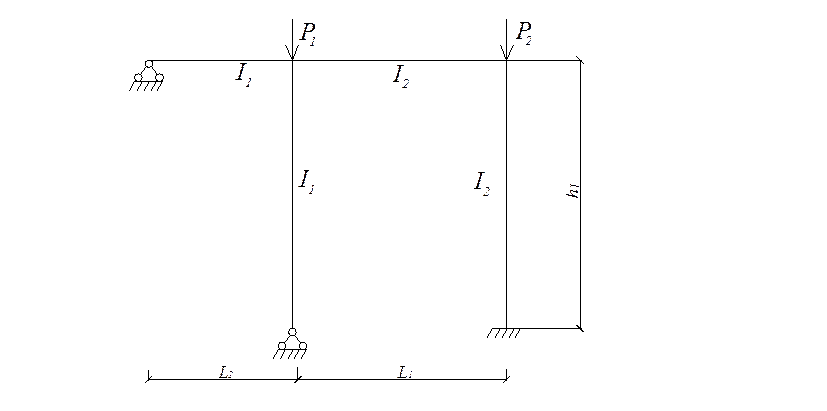
Дано:                              

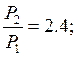
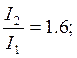
§ 1. Расчетная модель

1.1.  Описание физических свойств материала

Материал рамы – сталь Ст.3., модуль упругости

1.2.  Образование расчетной схемы

    

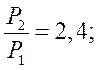
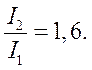
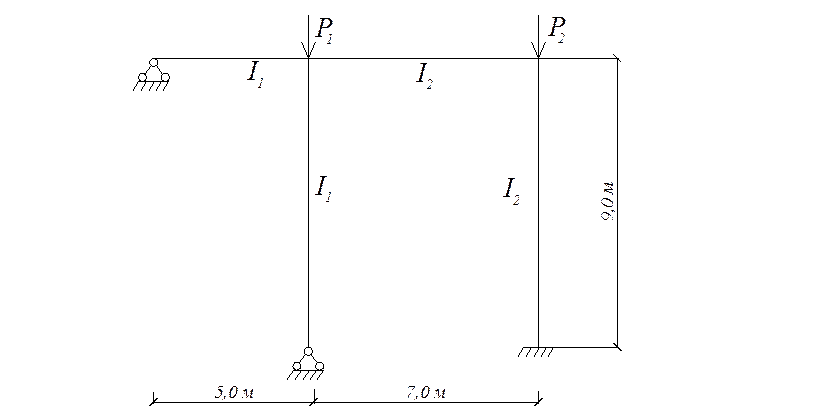
Рис 1. Расчетная схема рамы

1.3. Определение погонных жесткостей стержней рамы

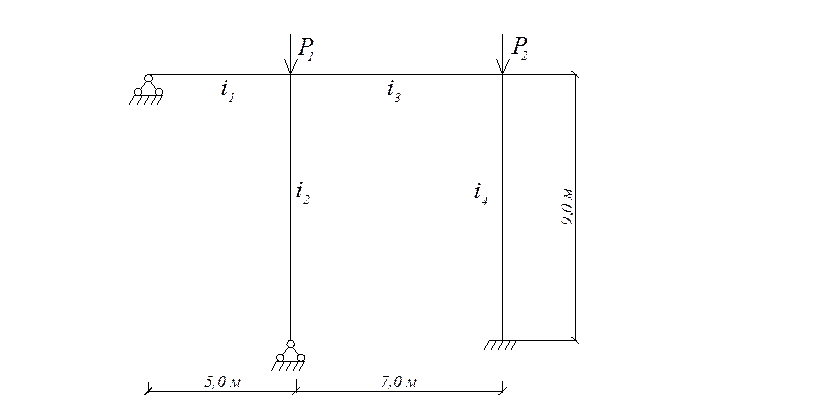
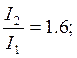 Тогда

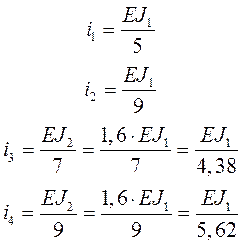
Примем  i₂  за типовую погонную жесткость.

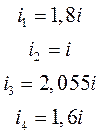
§ 2. Кинематический анализ расчетной схемы

2.1. Изображение расчетной схемы рамы в виде кинематической цепи

2.2. Подсчет числа степеней свободы

D = 1, У = 0, Ш = 0, С = 0, С_оп = 7

W= 3D + 2Y - 2Ш - С -  С_оп =3·1 - 7 = -4

Вывод: Система может быть статически неопределимой и геометрически неизменяемой.

2.3. Анализ геометрической структуры

Диск D₁ крепится к диску-земля  семью опорными стержнями, которые не параллельны друг другу и не пересекаются в одной точке, образуя с ним единый диск, следовательно, вся система образует единый диск.

2.4. Вывод о кинематических и статических свойствах расчетной схемы рамы

На основании подсчета числа степеней свободы и анализа геометрической структуры можно сделать вывод, что система является геометрически неизменяемой и статически неопределимой.

§ 3. Определение степени кинематической неопределимости  расчетной схемы

3.1. Определение числа неизвестных угловых перемещений

Число неизвестных угловых перемещений равно числу жестких узлов рамы, в нашем случае, n₁ = 2.

3.2. Определение числа неизвестных линейных перемещений

Введем вместо жестких узлов рамы шарниры. Число неизвестных линейных перемещений будет равно числу возможных линейных перемещений полученной системы, в нашем случае, n₂ = 0.

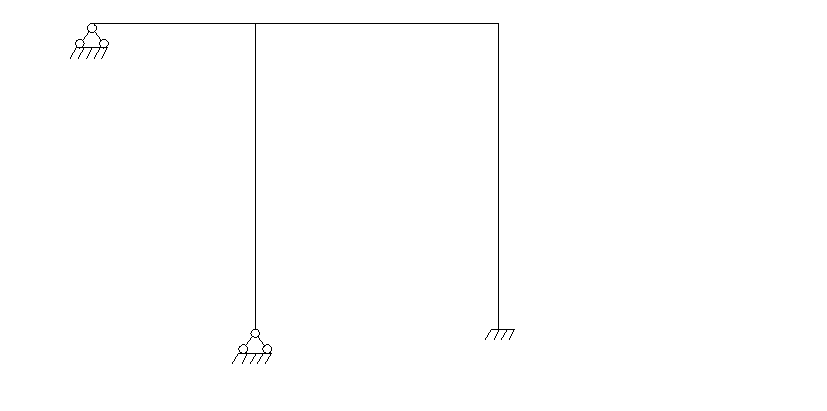
3.3. Определение степени кинематической неопределимости  расчетной схемы рамы  с учетом допущений и изображение расчетной схемы рамы с неизвестными перемещениями

Степень кинематической неопределимости расчетной схемы рамы равна полному числу неизвестных перемещений

n = n₁ + n₂ =  2 + 0 = 2.

Рис.2 Расчетная схема рамы с неизвестными перемещениями

§ 4. Определение критической нагрузки

4.1. Изображение расчетной схемы рамы с заменяющей системой узловых сил в критическом состоянии

Рис.3 Расчетная схема рамы с заменяющей системой узловых сил в критическом состоянии

4.2. Изображение основной системы метода перемещений в критическом состоянии

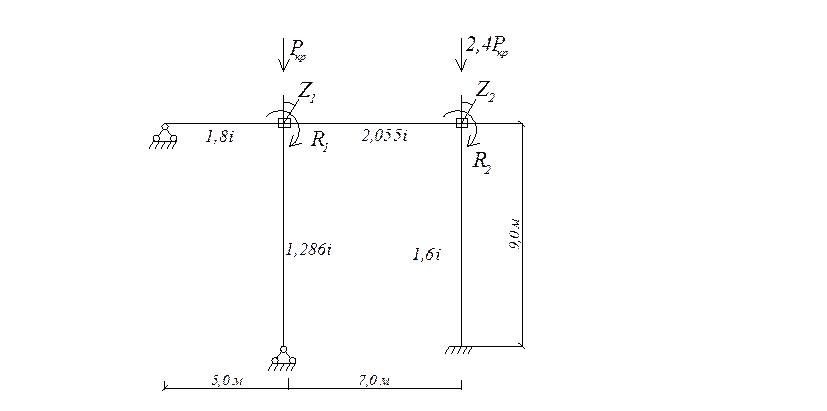
Рис.4 Основная система метода перемещений в критическом состоянии

4.3. Составление канонических уравнений метода перемещений в критическом состоянии

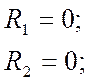
где  - параметр устойчивости сжатого стержня.

Определим параметры устойчивости сжатых стержней и выразим их через типовой параметр :

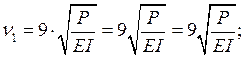
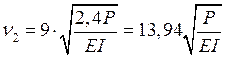
4.4. Изображение единичных состояний метода перемещений в критическом состоянии и построение эпюр  и

Единичное состояние Z₁

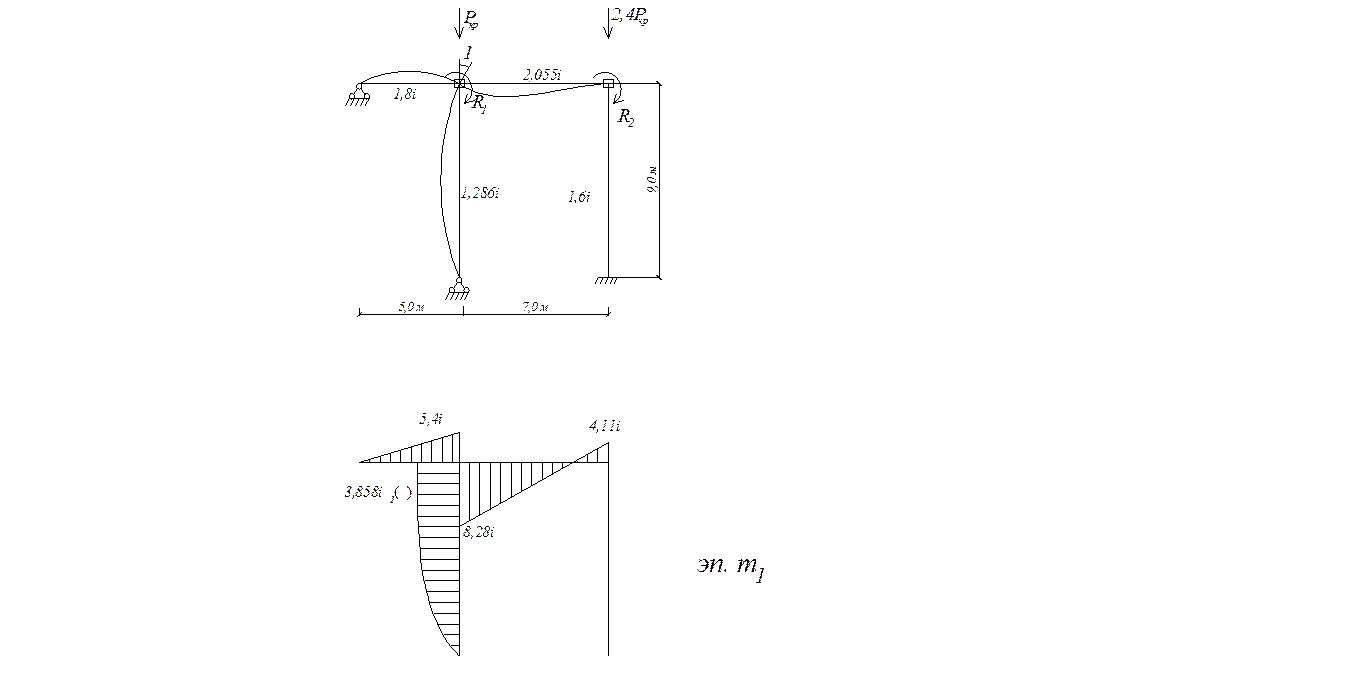
Единичное состояние Z₂

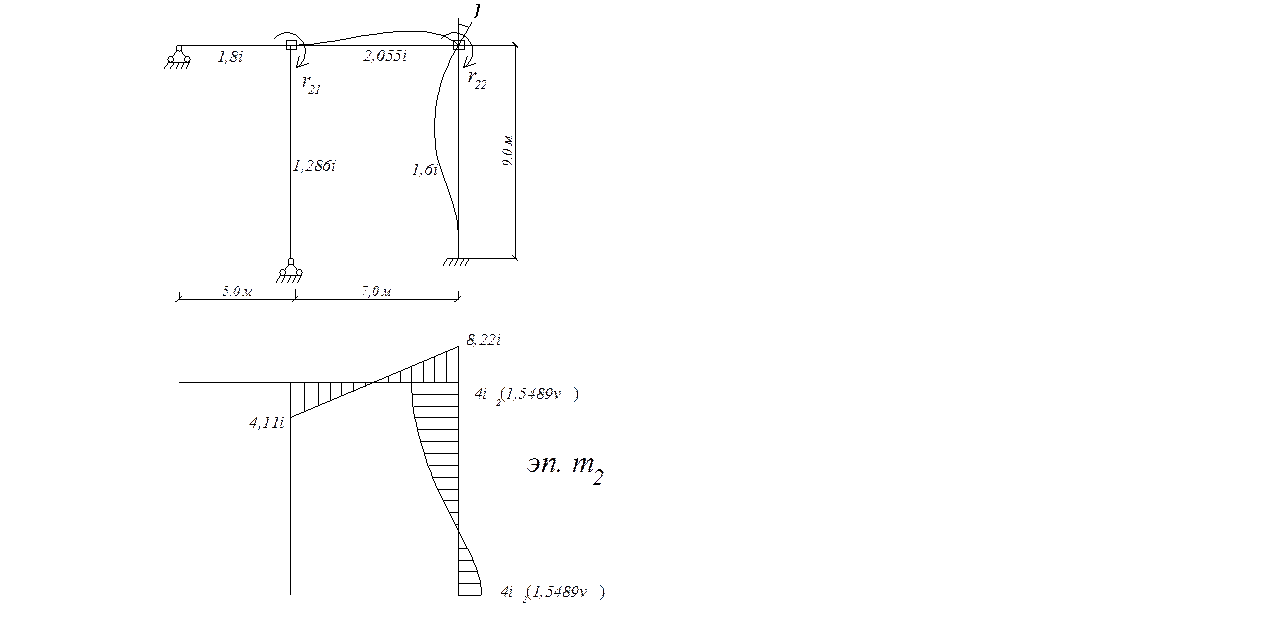
4.5. Вычисление коэффициентов канонических уравнений

Единичное состояние Z₁

           

        

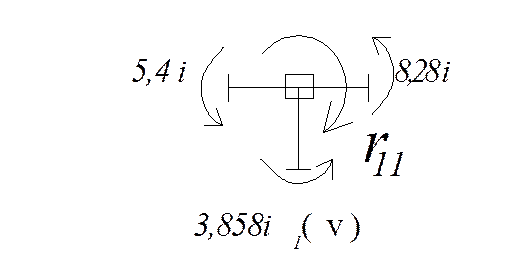
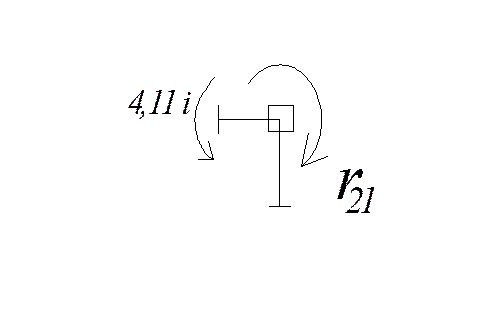
Единичное состояние Z₂

           

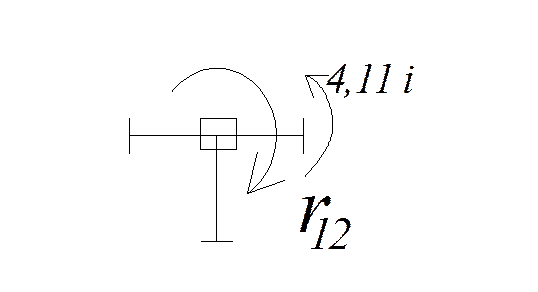
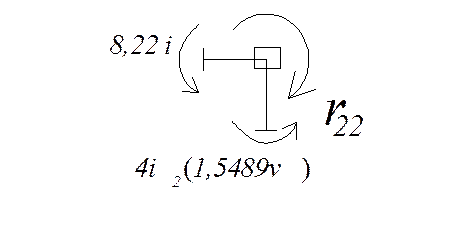
4.6. Составление уравнения, описывающего достижение рамой критического состояния

Подставляем найденные коэффициенты в уравнения метода перемещений в критическом состоянии

Данная система уравнений имеет два решения:

1)  - тривиальное решение, существующее при (в этом случае форма равновесия является устойчивой по Лагранжу) и при  (в этом случае форма равновесия является неустойчивой);

2)  - нетривиальное решение, существующее при и описывающее смежную форму равновесия.

Условием существования является равенство 0 определителя системы канонических уравнений:

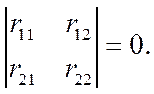
Подставим найденные коэффициенты в определитель системы канонических уравнений:

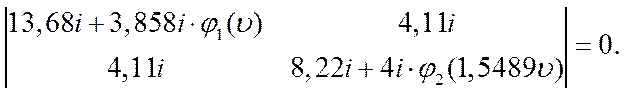
Раскроем определитель и получим уравнение,описывающее достижение рамой критического состояния:

4.7. Нахождение с помощью ЭВМ параметра низшей критической нагрузки рамы

Графическое отделение наименьшего корня

§ 5. Определение расчетных длин стоек

5.1. Определение для каждой стойки величины безразмерного параметра нагружения в критическом состоянии

5.2. Определение расчетных длин стоек

Для определения расчетных длин стоек определим коэффициенты :

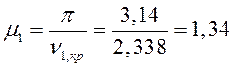
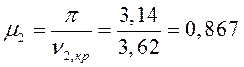
Расчетные длины стоек будут равны