Строительство и архитектура \ Железобетонные конструкции

Расчет монолитной железобетонной фундаментной плиты. Определение усилий на фундамент от крайних колонн. Определение усилий на фундамент от средней колонны. Определение эпюр реактивных давлений грунта, изгибающих моментов и поперечных сил от расчетных нагрузок, страница 4

ξ

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

0

0,024

-0,01

-0,032

-0,036

-0,033

-0,026

-0,018

-0,01

-0,003

0

M1

0

1719,1

-1146

-2292,1

-2578,1

-2363,2

-1862,2

-1289,2

-716,25

-214,8

0

ξ

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

0

-0,003

-0,01

-0,018

-0,026

-0,033

-0,036

-0,032

-0,016

0,024

0

M2

0

-305,4

-1018

-1832,7

-2647,3

-3360,1

-3665,5

-3258

-1629,1

2443,6

0

ξ

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

0

0,003

0,013

0,034

0,065

0,109

0,065

0,034

0,013

0,003

0

M3

0

592,66

2568,2

6716,9

12841,7

21533,6

12841,1

6716,9

2568,2

592,66

0

Берем алгебраическую сумму M=M1+ M2+ M3, и получим :

ξ

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

M

0

2006,2

404,03

2592,19

7615,35

15809,9

7313,4

2169,44

222,86

2821,6

0

Строим эпюру изгибающих моментов:

Эпюра М

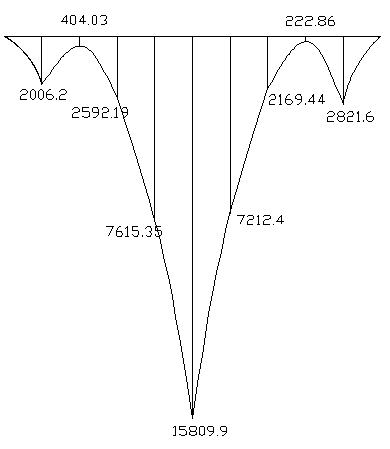
Определяем площадь продольной арматуры от действия максимального момента.

Сечение монолитной плиты b=6600мм, в месте действия максимального момента примем  h=1200мм, c=50мм.

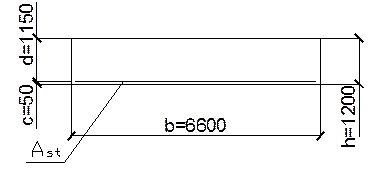Бетон тяжелый класса С20/25(fck=20 мПа, γс=1,5; fcd=fck/γc=20/1.5=13,33 мПа). Арматура класса S500(fyk=500мПа, fyd=450мПа).Изгибающий момент, действующий в сечении Мsd =1580,9 кН·м.

Определяем величину коэффициента αm: 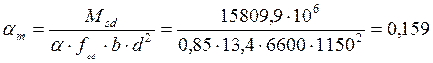Определяем относительную деформацию арматуры, для арматуры S500 при ES=20·104 мПа:

;

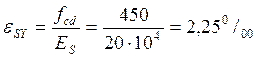Определяем граничную величину коэффициента αm,lim:

αm,lim=ωC·ξlim·(1-k2·ξlim);

где: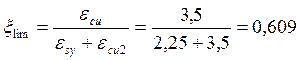

Для бетона С20/25  εcu=3,5; ωC=0,81; k2=0,416

Получаем:

αm,lim=0,81·0,609(1-0,416·0,609)=0,368;

Поскольку условие выполняется: αm=0,159< αm.lim=0,368 , растянутая арматура достигла предельных деформаций.

Тогда при 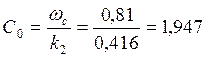 находим η:

;

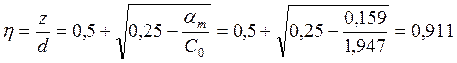Определим величину требуемой площади растянутой арматуры:

 

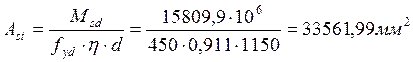
Принимаем: 70Æ25 S500  (Аst=34363,3 мм2).

Определяем площадь продольной арматуры от крайних моментов.

Определяем величину коэффициента αm: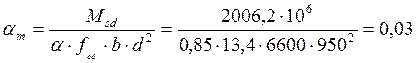

Определяем относительную деформацию арматуры, для арматуры S500 при ES=20·104 мПа:

;

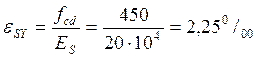Определяем граничную величину коэффициента αm,lim:

αm,lim=ωC·ξlim·(1-k2·ξlim);

где: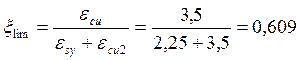

Для бетона С20/25  εcu=3,5; ωC=0,81; k2=0,416

Получаем:

αm,lim=0,81·0,609(1-0,416·0,609)=0,368;

Поскольку условие выполняется: αm=0,233< αm.lim=0,368 , растянутая арматура достигла предельных деформаций.

Тогда при 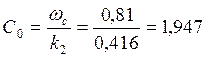 находим η:

;

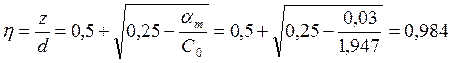Определим величину требуемой площади растянутой арматуры:

 

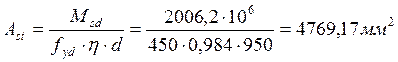
Принимаем: 20Æ18 S500  (Аst=5090 мм2).

Определяем величину коэффициента αm от следующего крайнего момента: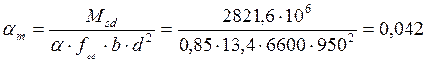

Определяем относительную деформацию арматуры, для арматуры S500 при ES=20·104 мПа:

;

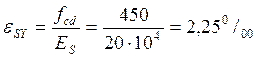Определяем граничную величину коэффициента αm,lim:

αm,lim=ωC·ξlim·(1-k2·ξlim);

где: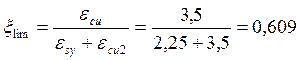

Для бетона С20/25  εcu=3,5; ωC=0,81; k2=0,416

Получаем:

αm,lim=0,81·0,609(1-0,416·0,609)=0,368;

Поскольку условие выполняется: αm=0,233< αm.lim=0,368 , растянутая арматура достигла предельных деформаций.

Тогда при  находим η:

;

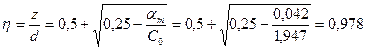Определим величину требуемой площади растянутой арматуры:

 

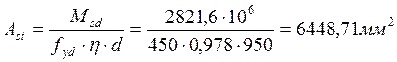
Принимаем: 30Æ18 S500  (Аst=7635 мм2).

Для определения величины длины анкеровки стержней в месте действия максимального момента, строим эпюру материалов.

Найдем величины моментов от действия крайних сил по формуле:

Msd=Ast·fsd·η·d; 

Msd1=5090·450·0,984·950=2132455,5кН/мм=2132,4 кН/м

Msd2=7635·450·0,978·950=3192155,3кН/мм=3192,155кН/м

Msd3=34363,3·450·0,911·1150=16200320,06кН/мм=16200,32кН/м

Определяем длину анкеровки:

qsw1=450·50,9/30=763,5

W1=41248/2·763,5+5·95=402,01см

qsw1=450·76,35/30=1145,25

W2=332997/2·1145,25+5·95=485,38см

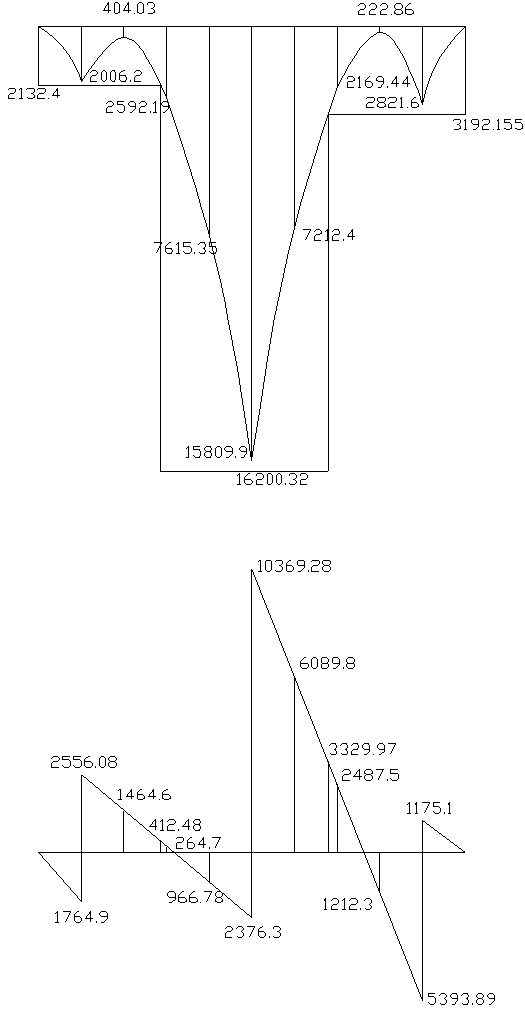
На основании полученных данных строим эпюру материалов.

Эпюра материалов:

Скачать файл