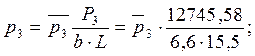Строительство и архитектура \ Железобетонные конструкции

Расчет монолитной железобетонной фундаментной плиты. Определение усилий на фундамент от крайних колонн. Определение усилий на фундамент от средней колонны. Определение эпюр реактивных давлений грунта, изгибающих моментов и поперечных сил от расчетных нагрузок, страница 3

Для определения ординаты p3 от силы P3 берем из таблицы III.1 данные , соответствующие  β3 =0,5, α=223,74 , для всех значений от  ξ =0 до ξ =1.Умножив каждую ординату согласно формуле :

ξ

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

0,486

0,764

0,976

1,134

1,226

1,257

1,226

1,134

0,979

0,764

0,48

p3

60,550

95,186

121,60

141,28

152,7

156,60

152,74

141,28

121,97

95,186

60,5

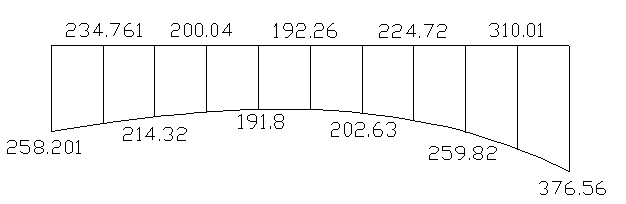
Пользуясь принципом независимости действия сил, для получения величины p берем алгебраическую сумму p= p1+ p2+ p3, и получим :

ξ

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

p

258,20

234,76

214,32

200,04

191,8

192,26

202,63

224,72

259,82

310,01

376,56

Строим эпюру реактивных давлений:

Эпюра P :

Для сравнения с характеристиками грунта, определим расчетное сопротивление грунта.   Расчетное сопротивление грунта определяется по формуле:

 ;

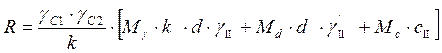где:  γС1 и γС2 –коэффициенты условия работы, γС1=1,2 , γС2 =1;

k– принимается равный  1,1 и зависит от коэффициенты условия работы ;

Мγ,Мd,МС –моменты действующие в плоскости обреза фундамента;

d– глубина заложения фундамента от уровня планировки;

с2 – удельное сцепление грунта;

γII(γ’II)–средневзвешенное значение удельного веса грунта, определяется по формуле:

;

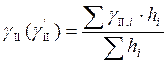где :  hi – расчетная толщина слоев грунта;

γII– удельный вес грунта, γII=16,8кН/м

;

 ;

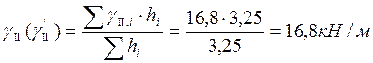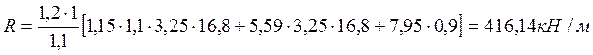На основании полученных данных, мы можем увидеть  что расчетное сопротивление грунта больше значения реактивного давления, следовательно грунт нести приложенную на него нагрузку без разрушительных деформаций.  

Действуя аналогично, определяем ординаты Q:

Для определения поперечной силы Q, также из таблицы 3.2(И.А. Симвулидий „Расчет инженерных конструкций на упругом основании ”) берем данные соответствующие  α= =223,74; β1 =0,074; β2 =0,5;  β3 =0,926, для всех значений ξ от нуля до единицы.

Умножив каждую ординату согласно формуле, получим:

ξ

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

0

0,449

-0,264

-0,091

0,007

0,056

0,076

0,077

-0,07

-0,053

0

Q1

0

2074,8

-1219,9

-420,5

32,346

258,77

351,195

355,81

-360,4

-244,9

0

ξ

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

0

-0,053

-0,078

-0,083

-0,077

-0,056

-0,088

-0,091

-0,364

-0,551

0

Q2

0

-348,15

-512,38

-545,2

-505,8

-367,8

-578,07

-597,7

-2391,1

-3619,5

0

ξ

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

0

0,003

0,021

0,055

0,113

0,195

-0,46

-0,33

0,311

0,211

0

Q3

0

38,236

267,657

701,01

1440,2

2485,3

-5862,9

-2245

3963,8

2689,3

0

Берем алгебраическую сумму Q=Q1+ Q2+ Q3, и получим :

ξ

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

Q2

0

1764,9

-1464,6

-264,7

966,7

2376,3

-6089,8

-2487,5

1212,3

-1175,1

0

-2556,1

-10369,2

5393,8

Строим эпюру поперечных сил:

Эпюра Q:

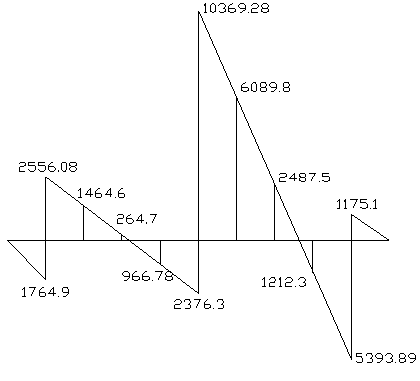
Для определения изгибающих моментов  М,  из таблицы 3.3(И.А. Симвулидий „Расчет инженерных конструкций на упругом основании ”) берем данные соответствующие  α= =223,74; β1 =0,074; β2 =0,5;  β3 =0,926, для всех значений ξ от нуля до единицы.

Умножив каждую ординату согласно формуле, получим:

Скачать файл