Расчёт и конструирование железобетонной лестницы из мелкоразмерных элементов, страница 5

Длину проекции наклонной трещины l_inc,cr, определяющей поперечное усилие V_sd, воспринимаемое поперечными стержнями, принимаем равной наименьшему значению из трёх величин:

1)  l_inc=2·d=2·37,5=75,0см

2) Вычисляем:

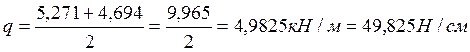, значение l_inc вычисляем по формуле: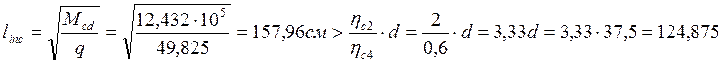

При этом составляющая поперечной силы, воспринимаемая сечением над вершиной наклонной трещины:

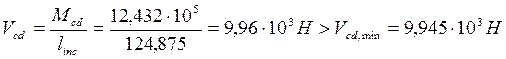
Величина поперечная силы в вершине наклонной трещины равна:

Длина проекции расчётного наклонного сечения l_inc,cr:

3) 

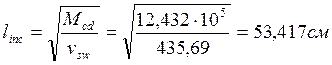
l_inc -т.к. условие выполняется, то принимаем значение l_inc,cr=53,417см.

Вычисляем поперечную силу V_sv, воспринимаемую поперечными стержнями в наклонном сечении по формуле:

Проверяем условие прочности в расчётном наклонном сечении:

-- условие выполняется, следовательно, поперечной арматуры, принятой по расчёту, для восприятия поперечных сил достаточно.

Проверка прочности бетона по сжатой полосе между наклонными трещинами:

 

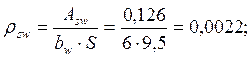
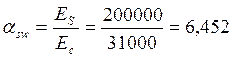
Условие

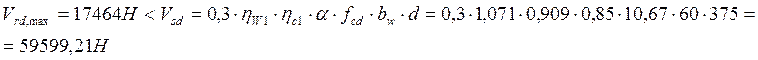
Условие удовлетворяется, следовательно, прочность по наклонной полосе между диагональными трещинами обеспечена.

3.2.4.5 Расчет L-образного косоура по трещиностойкости

Момент в расчётном сечении от практически постоянной комбинации равномерно распределённых нагрузок:

qⁿ  =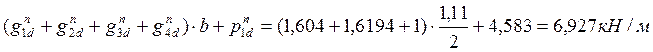

равен:

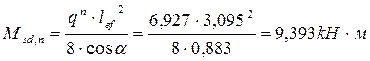
По таблице 10.1 [3] для класса Х0 предельно допустимая ширина раскрытия трещин .

Геометрические размеры сечения примем равными 60х390мм, толщина защитного слоя – 15 мм.

Арматура класса S400 (). Диаметр продольной арматуры – 1ø12мм S400 с А_S1=1,313см², диаметр поперечной арматуры – Ø_sw=4мм с площадью А_sw= 0,126см².

Бетон класс С16/20 ( , модуль упругости  (для марки по подвижности П1).

Рабочая высота сечения

Ø_sw-Ø/2=390-15-4-12/2=365мм

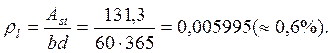
Проверяем ширину раскрытия трещин по упрощённой методике, пользуясь данными  таблицы 10.2 [3]. Для сечений прямоугольной формы, армированных арматурой класса S400 при 0,5%  плечо внутренней пары сил определяется:

Напряжения в растянутой арматуре определяем по формуле (10.19) [3]:

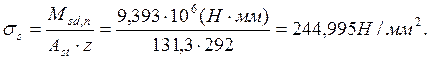
По таблице 10.2 [3] Ø_max=20 мм при  и .

Принятый диаметр Ø=12мм< Ø_max=20 мм.

Проверим ширину раскрытия трещин расчётным путём. Учитывая то обстоятельство, что момент  рассчитан на практически постоянной комбинации равномерно распределённых нагрузок, при проверке ширины раскрытия трещин используем эффективный модуль упругости:

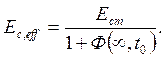
Предельное значение коэффициента ползучести  определим из номограммы, приведённой на рис. 4.16 [3]. При 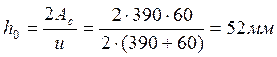 и  для сут.

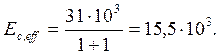
Коэффициент привидения .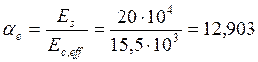

Для сечений с трещиной при использовании двухлинейной диаграммы деформирования высота сжатой зоны в общем случае может быть найдена из условия равенства статических моментов сжатой и растянутой зон сечения относительно нейтральной оси:

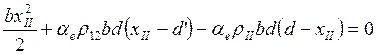
Тогда

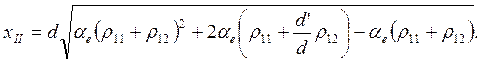
При отсутствии расчётной арматуры в сжатой зоне .

Подставляя значение получаем:

Напряжение в арматуре:

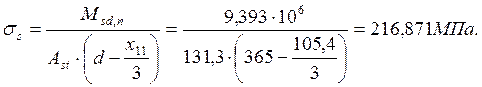
Расчётную ширину раскрытия трещин определяем по формуле:

, где S_rm – среднее расстояние между трещинами, определяемое по формуле:

∙Ø/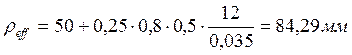 

при  (для стержней периодического профиля),  (при изгибе),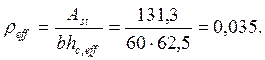

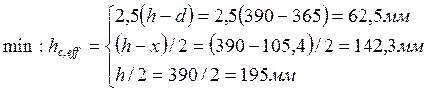
Средние относительные деформации арматуры  определим по формуле:

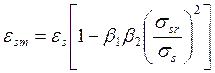
При (для стержневой арматуры), (для практически постоянной комбинации нагрузок);

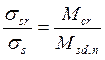
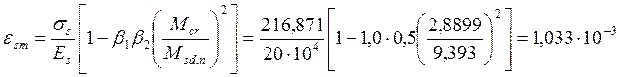
где -- момент трещинообразования

,

-- момент сопротивления бетонного сечения

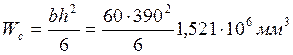
Тогда

Тогда при

Проверка по ширине раскрытия трещин выполняется.

3.2.4.6 Расчет L-образного косоура по деформациям

Максимальный прогиб в середине пролёта свободно опёртого косоура, загруженного равномерно распределённой нагрузкой:

qⁿ  =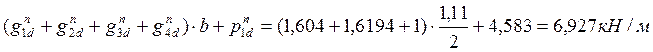

определим по формуле:

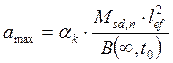
По таблице 11.1 [3] коэффициент ,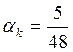

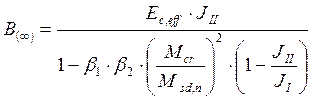
Для прямоугольного сечения

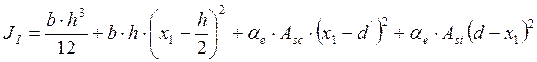
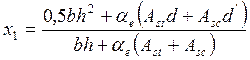
При A_sc=0

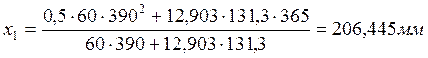, где коэффициент привидения .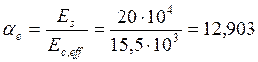

     

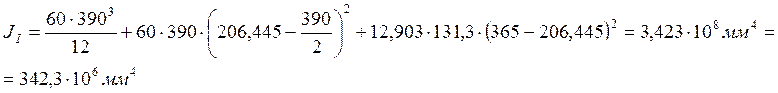
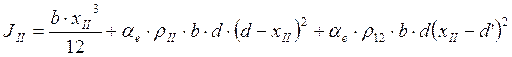
При  и  получаем:

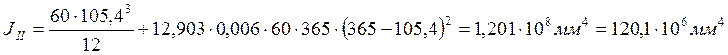
Жёсткость сечения с трещиной:

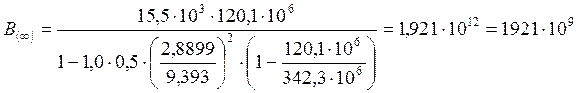
Прогиб в середине пролёта

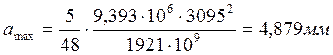
Допустимый прогиб

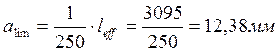
Максимальный прогиб в середине пролёта балки не превышает допустимый, т.е. проверка выполняется.