Расчёт и конструирование железобетонной лестницы из мелкоразмерных элементов, страница 4

     

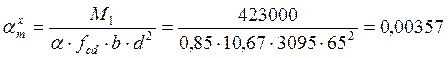
где d – высота сжатой зоны бетона и равна:

d=80-15=65мм.

Определяем граничную величину коэффициента α_m,lim:

Поскольку выполняется условие  установка сжатой арматуры не требуется.

При  по таблице 6.7 [3] находим =0,991.

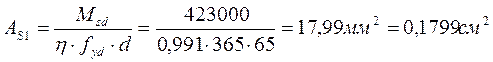
Согласно СНБ 5.03.01-02 “Бетонные и железобетонные конструкции” по конструктивным требованиям минимальное содержание арматуры S₁ в изгибаемых элементах принимаем 0,15% (таблица 11.1 [3]) от площади поперечного сечения бетона А_с.

                                                                              

Принимаем 2ø6мм S400 с А_S1=0,57см² с шагом 60мм.

3.2.4.4. Расчёт по прочности на действие поперечных сил

Расчёт железобетонных элементов по прочности на действие поперечных сил при отсутствии вертикальной и наклонной арматуры, следует производить из условия:

 – расчётная поперечная сила в рассматриваемом сечении, вызванная действием нагрузок;

 – расчётная поперечная сила, воспринимаемая железобетонным элементом без поперечной арматуры.

Расчётную поперечную силу  следует определять по формуле:

, но не менее ,                                                          

где 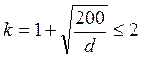 , d – в мм;                                                                                          

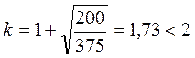, т.к. неравенство выполняется, принимаем k=1,73.

                                                                                         

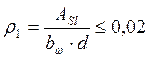
 – площадь сечения продольной растянутой арматуры, учитываемой в расчёте прочности наклонного сечения;

b_ω– минимальная ширина поперечного сечения элемента в растянутой зоне.

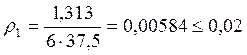
, т.к. косоур работает без действия на него предварительного напряжения, а осевое усилие, вызванное действием нагрузки отсутствует.

Для бетона

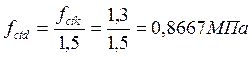
>, условие выполняется.

Для сравнения принимаем внутреннюю несущую способность

.

<

Условие прочности не выполняется, следовательно, требуется установка поперечной арматуры по расчёту.

Определим необходимость наличия поперечной арматуры в опорной части полки L-образного косоура.

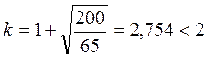, т.к. неравенство выполняется, принимаем k=2,754.

                                                                                         

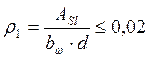
 – площадь сечения продольной растянутой арматуры, учитываемой в расчёте прочности наклонного сечения;

b_ω– минимальная ширина поперечного сечения элемента в растянутой зоне.

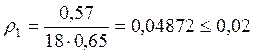
, т.к. косоур работает без действия на него предварительного напряжения, а осевое усилие, вызванное действием нагрузки отсутствует.

Для бетона

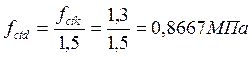
>, условие выполняется.

Для сравнения принимаем внутреннюю несущую способность

.

<

Условие прочности не выполняется, следовательно, требуется установка поперечной арматуры по расчёту.

3.2.4.4.1 Расчёт прочности по сечениям, наклонным к продольной оси

Диаметр поперечных стержней устанавливаем из условия сварки их с продольной арматурой, диаметр которой равен Ø=12мм, и принимаем равным Ø_sw=4мм с площадью А_sw= 0,126см². При классе поперечной арматуры S400 ;

Поскольку Ø_sw/ Ø = 4/9 = 0,444< 1/3, коэффициент условий работы g_s2 = 0,8, учитывающий возможность хрупкого разрушения сварного соединения. Коэффициент       g_s1 = 0,9, учитывающий неравномерность распределения напряжений в арматуре по длине рассматриваемого сечения. Таким образом  = 0,9х365=328,5МПа.

Шаг поперечных стержней по конструктивным условиям:

1.  На приопорных участках длиной 0,25·l, при h≤450 мм – не более 0,5h и 500 мм, S = h/3 = 197/2 = 98,5 мм, принимаем S=95мм.

2.  В средней части пролета независимо от высоты – не более 3/4h и 500мм,      

S = 3h/4 = 3·197/4 = 147,75мм, принимаем S=145мм.

Вычисляем:

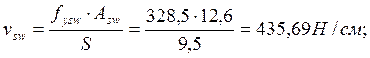
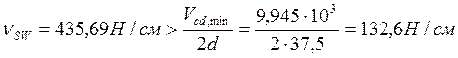- условие удовлетворяется.

Проверяем принятый шаг хомутов:

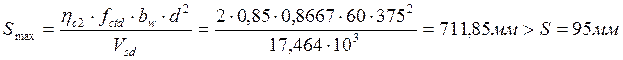 условие удовлетворяется, следовательно, шаг поперечной арматуры принят верно.

3.2.4.4.2. Расчет прочности по наклонному сечению