Вычисление двойных интегралов в прямоугольных координатах. Переход в двойных интегралах от прямоугольных координат к полярным. Геометрические и механические приложения двойных интегралов, страница 2

Опр: Число I называют пределом интегральных сумм (1) при λ→0 и пишут , если для любого ε>0 найдётся δ>0 такое, что для всех разбиений τ области Т на частичные области  T_k и не имеющих общих внутренних точек с условием  λ=λ_τ<δ  и для любого способа выбора промежуточных точек M_k выполняется неравенство |σ–I|<ε.

Опр: Если существует конечный предел интегральных сумм (1), то он называется тройным интегралом функции u=f(M) по области Т и обозначается . При этом ф–ция u=f(M) называется интегрируемой в области Т, а dV- элементарный объём в области Т.

24. Основные свойства 3-го интеграла.

1.2. - объем фигуры Т.

3. Если ф–ция u=f(M) непрерывна в кубируемой области Т, то она интегрируема в этой области.

4. Свойство адитивности Если T=T₁ÈT₂, T₁ и T₂ не имеют общих внутренних точек, то .

5. Свойство линейности .

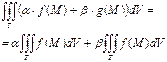6. Если f(M) и g(M) интегрируемы в Т, то и  f(M)^.g(M) так же интегрируема в Т.

7. Если  f(M) и g(M) интегрируемы в Т и всюду в Т f(M)£g(M), то .

8. Если  f(M) интегрируема в Т и всюду в Т m£ f(M)£ k, то

9. Если  f(M) интегрируема, в замкнутой области Т существует точка M₀ такая, что  - формула среднего значения.

25. Вычисление 3-х интегралов в прямоугольных координатах.

Пусть Т - произвольная фигура, ограниченная снизу поверхностью z=h₁(x,y), а сверху поверхностью  z=h₂(x,y), где  h₁(x,y) и h₂(x,y) - функции, непрерывные в области D, а с боков цилиндрической поверхностью, направляющей которой является граница области D..

Такая Т называется правильной в направлении оси Oz. z=h₁(x,y) –поверхность входа в Т. z=h₂(x,y) - поверхность выхода из Т.

Аналогично определяются фигуры, правильные в направлении осей Оу и Ох.

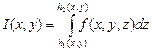Теорема: Пусть Т пространственная область правильная в направлении оси Oz. . u=f(x,y,z) - функция интегрируемая в Т. Если для каждой точки P(x,y) из D существует обычный определённый интеграл  (1), то существует  и интеграл 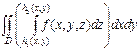 (2), а он равен тройному интегралу  (3).

Следствие: Если D={(x,y): a£x£b,φ₁(x)£y£φ₂(x)} и при любом  xЄ[a,b] существует 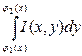, то (2) принимает вид  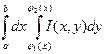и следовательно (3) примет вид  (4). Левая часть равенства (4) называется трёхкратным интегралом.

Следствие2: Если D={(x,y): c£y£d,ψ₁(y)£x£ψ₂(y)} и при любом  yЄ[c,d] существует 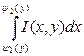, то (2) примет вид  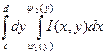и (3) примет вид  (5).

Замечание: Если пространственная область Т является правильной в другом направлении то возникнут еще 4 трёхкратных интеграла и еще 4 формулы, аналогичные формулам (4) и (5).

26. Переход в тройных интегралах от прямоугольных координат к цилиндрическим и сферическим.

Переход в тройном интеграле к цилиндрическим координатам.

Пусть определена система координат Oxyz, а на плоскости Оху задана ещё полярная система координат, стандартным образом совмещённая с прямоугольной.

Опр: Цилиндрическими координатами точки M(x,y,z) называются числа ρ,θ,z, где ρ и θ полярные координаты проекции точки M на плоскость Oxy.

Очевидно справедливы соотношения .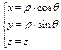

Элементарный объем преобразовывается так dV=ρdπdθdz.

Теорема: Если , где φ₁(θ) и φ₂(θ) – непрерывные функции на отрезке [a,b] и  f(x,y,z)ºF(ρ∙cosθ,ρ∙sinθ,z) интегрируема в Т, то 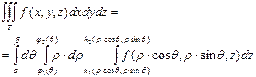 (1).

Правая часть называется трёхкратным интегралом.

Теорема:Если , где ψ₁(ρ) и ψ₂(ρ) непрерывны на отрезке [r,R] и функция  f(x,y,z)ºF(ρ∙cosθ,ρ∙sinθ,z) интегрируема в Т, то 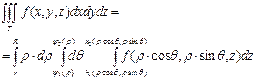 (2).

Переход в тройном интеграле к сферическим координатам.

Дана прямоугольная система координат Oxyz. Рассмотрим точку M(x,y,z). Пусть , r=|OM|, θ - угол в плоскости Oxy между осью Oх и вектором , φ - наименьший угол между осью Oz и вектором . r, φ, θ  - сферические координаты точки M. При этом r - радиус-вектор точки М, φ - широта точки М, а θ - долгота точки М.

Начало координат О имеет одну сферическую координату r=0, а φ и θ не определены. Точки оси Oz имеют две сферические координаты r, φ=0, а θ не определён.

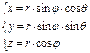
Покажем, что dV=r² sinφ dr dφ dθ - элементарный объём.

Теорема: Пусть область Т в пространстве Oxyz задаётся в сферических координатах следующим образом T={(r,φ,θ): α£θ£β, g₁(θ)£φ£g₂(θ),h₁(φ,θ)£r£ h₂(φ,θ)}, где функции g₁(θ), g₂(θ) непрерывны на отрезке [α,β], а функции h₁(φ,θ) и h₂(φ,θ) непрерывны в области . Пусть в Т задана функция  f(x,y,z)=f(r sinφ cosθ,r sinφ sinθ, r cosθ) интегрируема в Т. Тогда справедлива формула 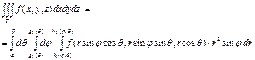Правая часть равенства называется трёхкратным интегралом в сферических координатах.