Физическая реализуемость (каузальность), стационарность, линейность и устойчивость цифровых цепей

Задание №1.

По заданным разностным уравнениям цифровых цепей проверьте и их физическую реализуемость (каузальность), стационарность, линейность и устойчивость.

			Вариант №4
Подвариант №4	а
	4

Рассмотрим некую систему с оператором  рис.1

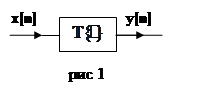
Проверим физическую реализуемость такой цепи, т.е. её каузальность.

Система называется каузальной, если  при  для любых ,   для .

Итак, имеем:

Возьмем  и  такие, что: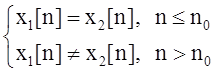 

тогда отклики системы:

Очевидно что при :

.

Пусть:

тогда

  только при , т.е. , что не соответствует определению каузальности.

Следовательно, система физически нереализуема, т.е. некаузальна.

Проверим стационарность цепи.

Цепь называется стационарной, если для неё выполняется свойство:

Если , то  .

Таким образом:

Найдем теперь:

, очевидно что:

, значит ,  что говорит о нестационарности цепи.

Проверяем линейность:

Система линейна тогда и только тогда, когда:

 

Имеем:

Найдем:

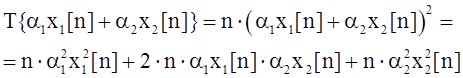
Запишем свойство:

Очевидно что правая и левая части выражения не равны, т.е. свойство   не выполняется, значит цепь нелинейна.

Проверяем устойчивость:

Система устойчива, если каждый ограниченный входной сигнал порождает  ограниченный выходной.

Пусть   и  , тогда:

В последнем выражении при  член  ограничен, а  – бесконечен, следовательно,  тоже бесконечно (неограниченно).

Значит цепь неустоичива.

В итоге имеем некаузальную нестационарную нелинейную неустойчивую цепь.

Задание №2. По разностному уравнению

§  Составьте структурную схему и постройте график импульсной характеристики (первые 10 значений) устойчивой дискретной цепи.

§  Рассчитайте АЧХ и ФЧХ цепи, постройте графики.

§  Постройте нуль-полюсную диаграмму, обозначьте область сходимости        z–преобразования ИХ.

Вариант
4	8.4	2	2
Подвариант
1	1	9	2

Составим структурную схему цепи, для этого выразим:

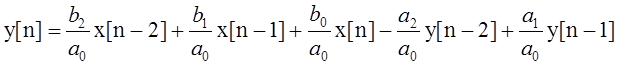
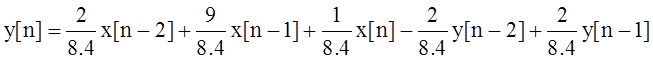
В итоге получим:

По полученному составим схему:

Для построения нуль-полюсной диаграммы и определения области сходимости найдем передаточную функцию цепи:

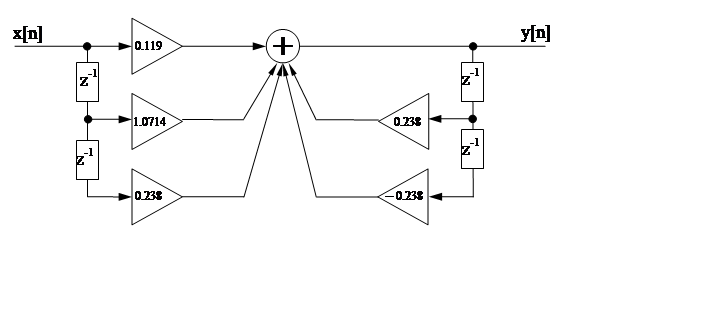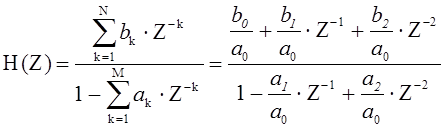
По основной теореме алгебры:

;

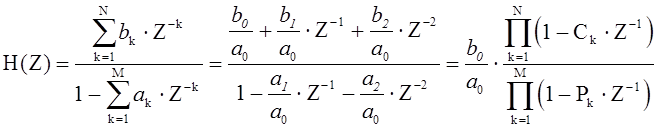Где N – число нулей передаточной функции (), M – число полюсов передаточной функции ().

Найдем и :

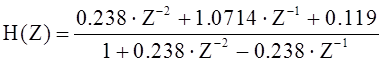
Решая уравнение получим нули:    .

Найдем полюсы:

Решая уравнение получим полюсы:    .

Построим нуль-полюсную диаграмму:

Поскольку , то для того чтобы цепь была устойчивой область сходимости должна быть внешность круга, следовательно последовательность правосторонняя.

Тогда рассчитаем импульсную характеристику (первые 10 значений):

где входная последовательность: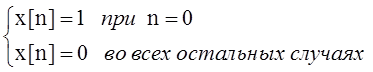

Получим:

  

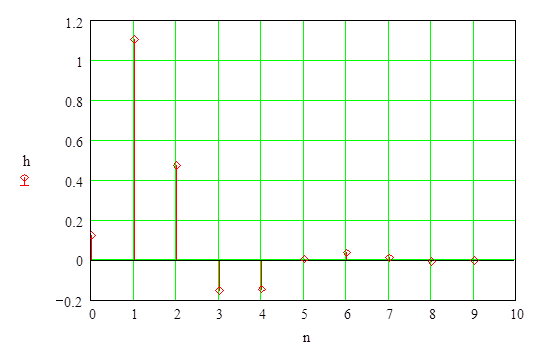
h[0] = 0.119

h[1] = 1.1

h[2] = 0.471

h[3] = -0.15

h[4] = -0.148

h[5] = 4.76 E-4

h[6] = 0.035

h[7] = 8.217 E-3

h[8] = -6.374 E-3

h[9] = -3.473 E-3

Построим АЧХ и ФЧХ:

АЧХ:

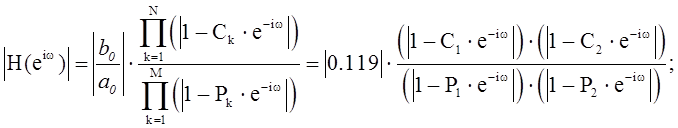
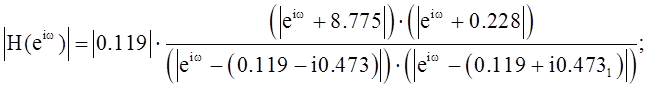
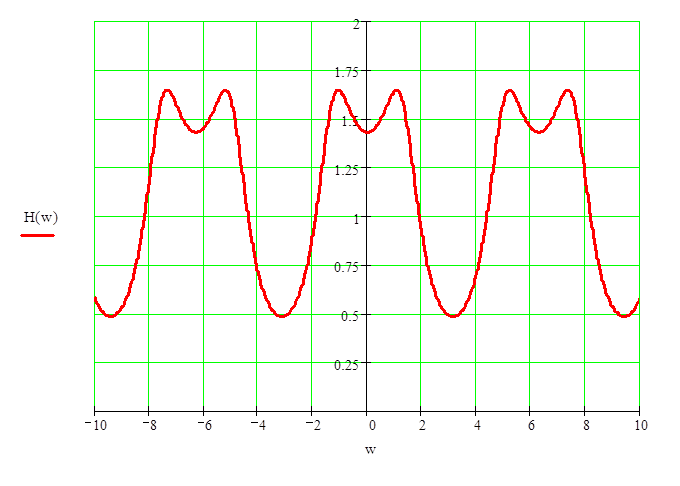
ФЧХ:

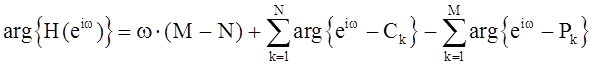
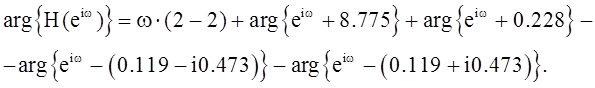
Литература.

1.  Конспект лекций по Цифровой обработке сигналов.

2.  Васюков В.Н. Введение в теорию ЦОС. Учебное пособие.