Расчет полосового цифрового фильтра

Министерство образования

Российской Федерации

НГТУ

Кафедра ТОР

Расчетно-графическое задание №2

«Расчет полосового цифрового фильтра»

Вариант №6

          Факультет: РЭФ

          Группа: РТС 9-92

          Студент: Соловьёв П.С.

          Преподаватель: Голещихин Д.В.

Новосибирск, 2002

Задание:

1.  Рассчитать полосовой фильтр (ПФ) 3 порядка (для четных вариантов – фильтр Чебышёва; для нечетных – фильтр Баттерворта).

Исходные данные:

§  частота дискретизации аналогового сигнала; нижняя и верхняя граничные частоты полосы пропускания, приведенные к частотам аналогового сигнала (табл.1);

§  преобразование ФНЧ в полосовой фильтр провести для аналогового фильтра;

§  аналого-цифровую трансформацию провести методом билинейного преобразования;

§  параметр  для фильтра Чебышёва принять равным 0.4.

2.  Построить структурную схему ЦФ в произвольной форме; коэффициенты фильтра не должны быть комплексными. Записать разностное уравнение ЦФ.

3.  Рассчитать и построить АЧХ, ФЧХ и ИХ цифрового фильтра.

Табл.1

Вариант	Частота,	Частота,	Частота дискретизации,
6	3000	6000	18000

Порядок фильтра N=3

1. Синтез аналогового ФНЧ-прототипа имеющего частоту среза .

Найдем частоты цифрового фильтра:

Сначала пересчитаем заданные частоты из рад/с в Гц:

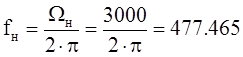, Гц   – нижняя частота

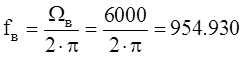, Гц  – верхняя частота

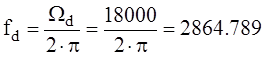, Гц  – частота дискретизации

Найдем параметры цифрового фильтра:

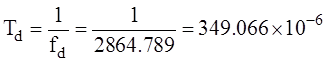, с  – период дискретизации

,  рад/с  – нижняя частота

,  рад/с – верхняя частота

Пересчитаем полученные частоты в частоты среза аналогового фильтра-прототипа:

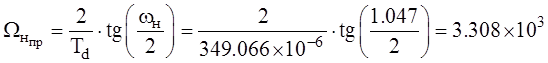 – нижняя частота;

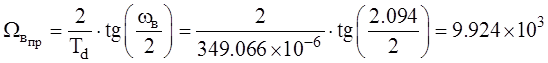– верхняя частота;

Нахождение полюсов:

Для устойчивого фильтра Чебышёва, полюсы лежат в левой части р-плоскости на эллипсе, заключенном между двумя окружностями радиусов а и b. Абсциссы полюсов определяются как абсциссы пересечения равностоящих по углу лучей с внутренней окружностью, а ординаты полюсов как ординаты  пересечения равностоящих по углу лучей с внешней окружностью, как показано на рис.1.

Где:

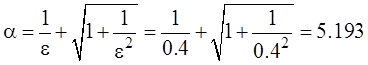
Радиусы окружностей:

;      

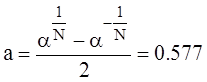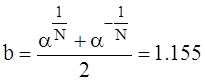
Таким образом, полюсы:

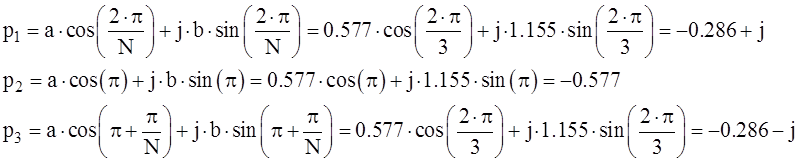
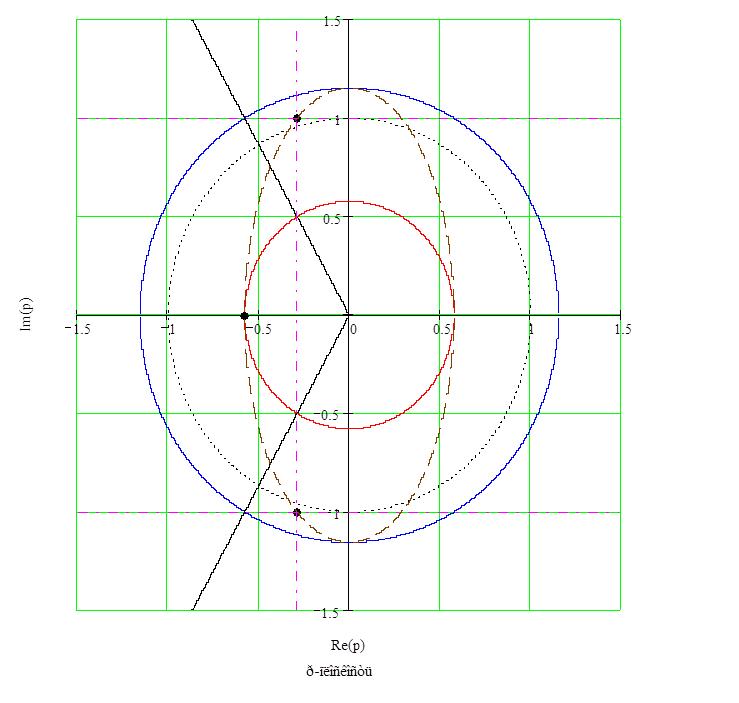
Рис. 1

Найдем передаточную функцию фильтра-прототипа:

; 

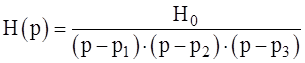Параметр найдем из следующего соображения: «Передаточная функция должна быть равна единице на нулевой частоте»   :

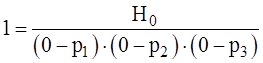, откуда:

В итоге имеем:

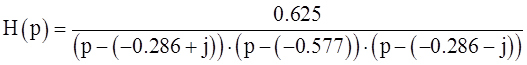
Построим АЧХ И ФЧХ фильтра-прототипа:

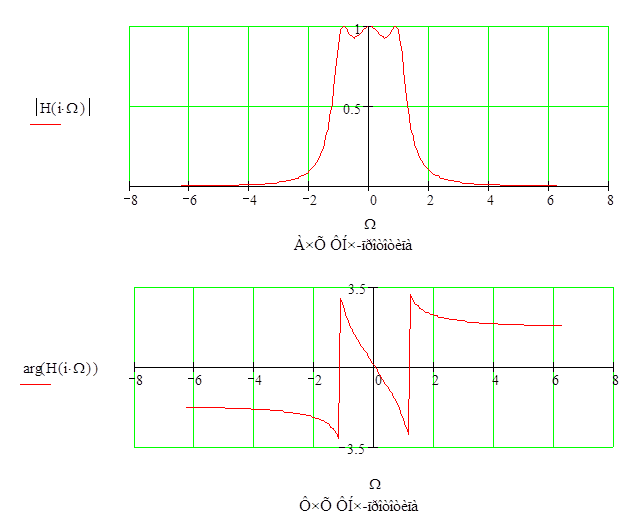
Рис. 2

Получим передаточную функцию аналогового полосового фильтра-прототипа:

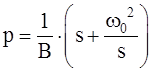Для преобразования ФНЧ в ПФ необходимо в  провести замену: ,где:

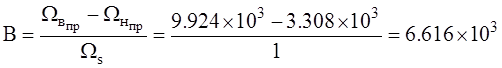
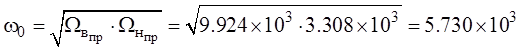
Таким образом:

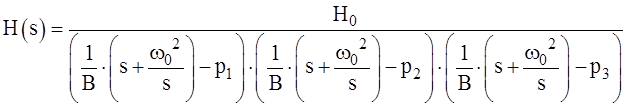
преобразуем:  

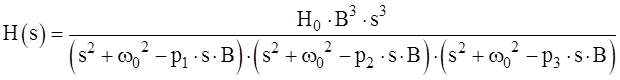
Далее раскроем скобки, приведем подобные, соберем коэффициенты при степенях s, и выпишем их:

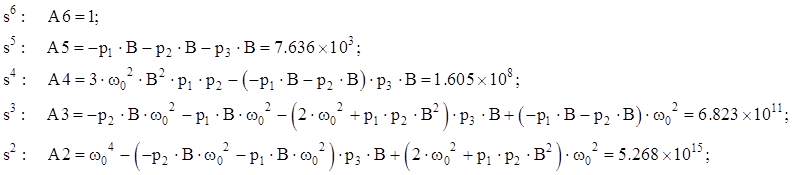
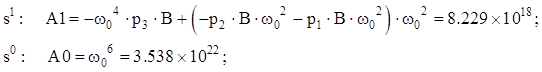
В итоге получим:

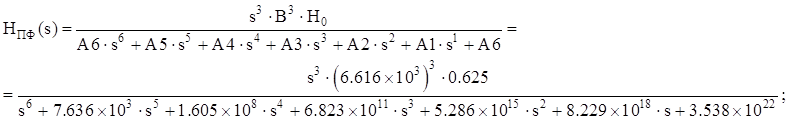
Построим АЧХ и ФЧХ полосового аналогового  фильтра:

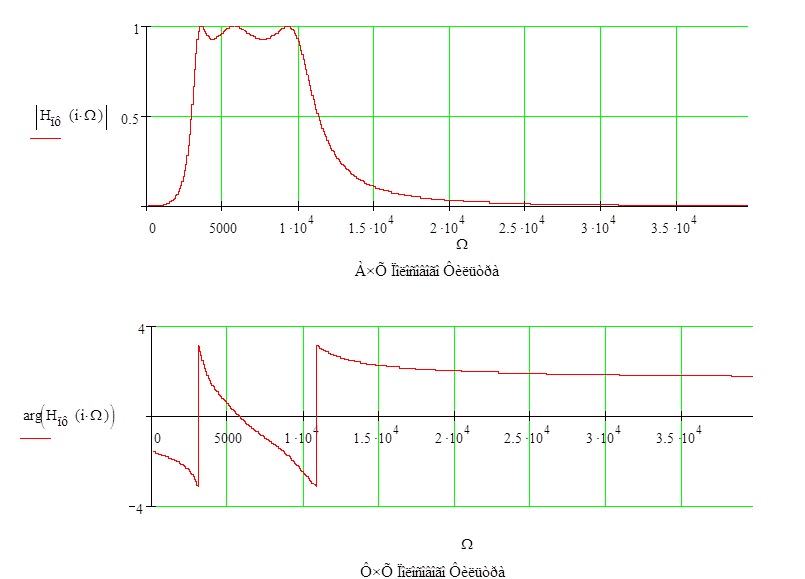
Рис. 3

2. Синтез цифрового фильтра методом билинейного преобразования.

Билинейное преобразование нелинейно трансформирует частотную ось так, что бесконечная ось аналоговых частот отображается на конечную ось дискретных частот.

Для проведения преобразования необходимо провести замену в H_ПФ(s):

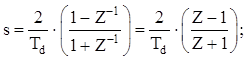
Для упрощения преобразований введем коэффициент ;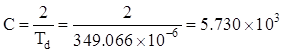

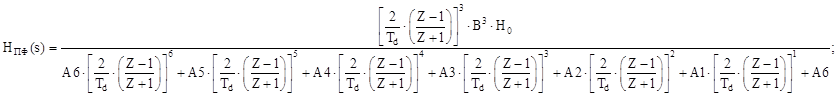
Далее раскроем скобки, приведем подобные, соберем коэффициенты при степенях и получим в итоге следующие коэффициенты:

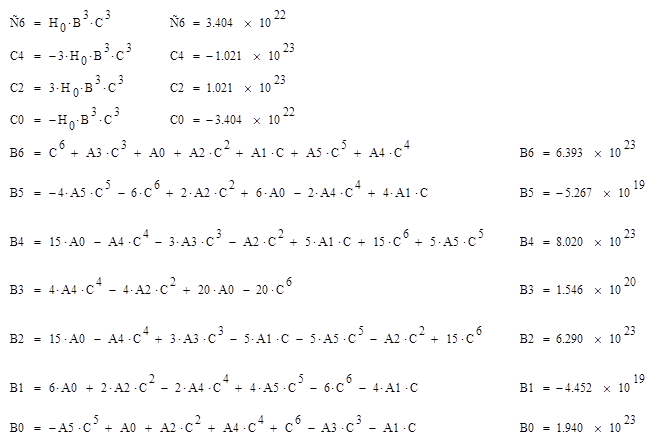
Тогда можем записать передаточную функцию в виде:

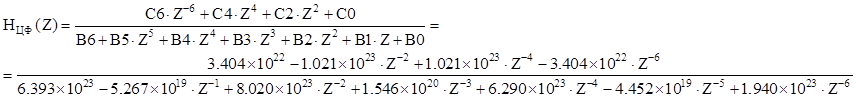
Построим АЧХ и ФЧХ полученного цифрового фильтра:

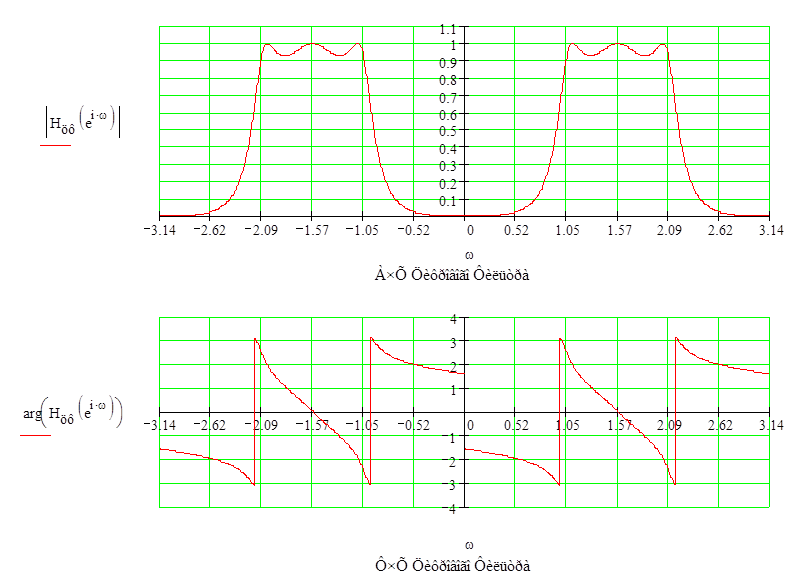
Рис. 4

По известной передаточной функции цифровой цепи составим её разностное уравнение и построим структурную схему.

Разностное уравнение:

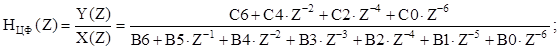
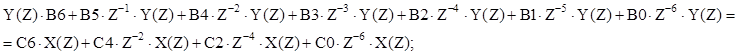
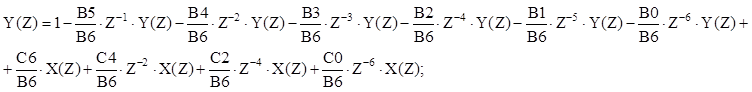
В итоге:

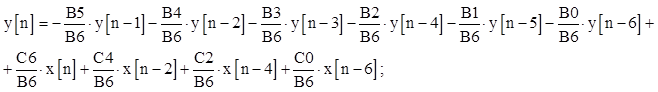
Разностное уравнение имеет вид:

y[n]

Структурная схема в канонической форме.

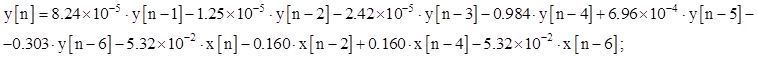
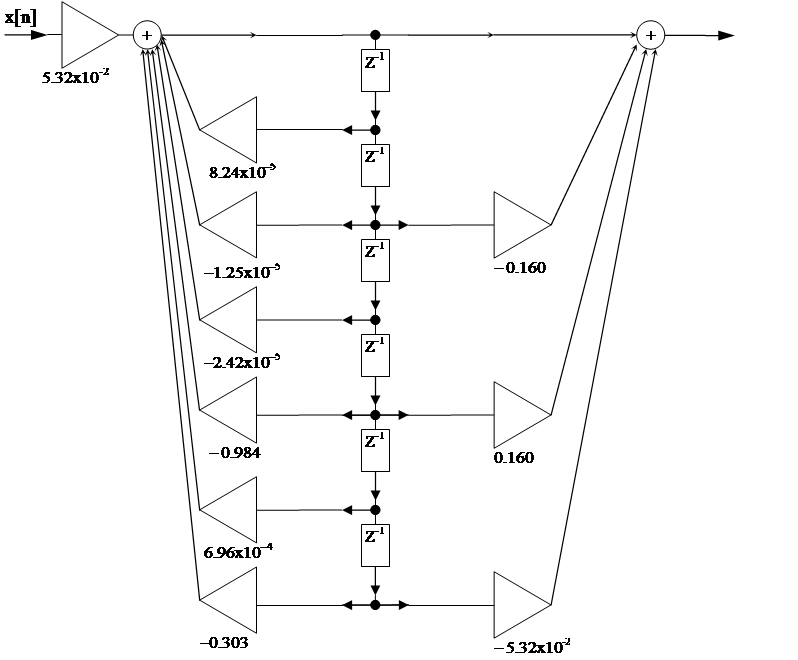
Рис.5 Структурная схема ЦФ.

3. Расчет и построение ИХ цепи.

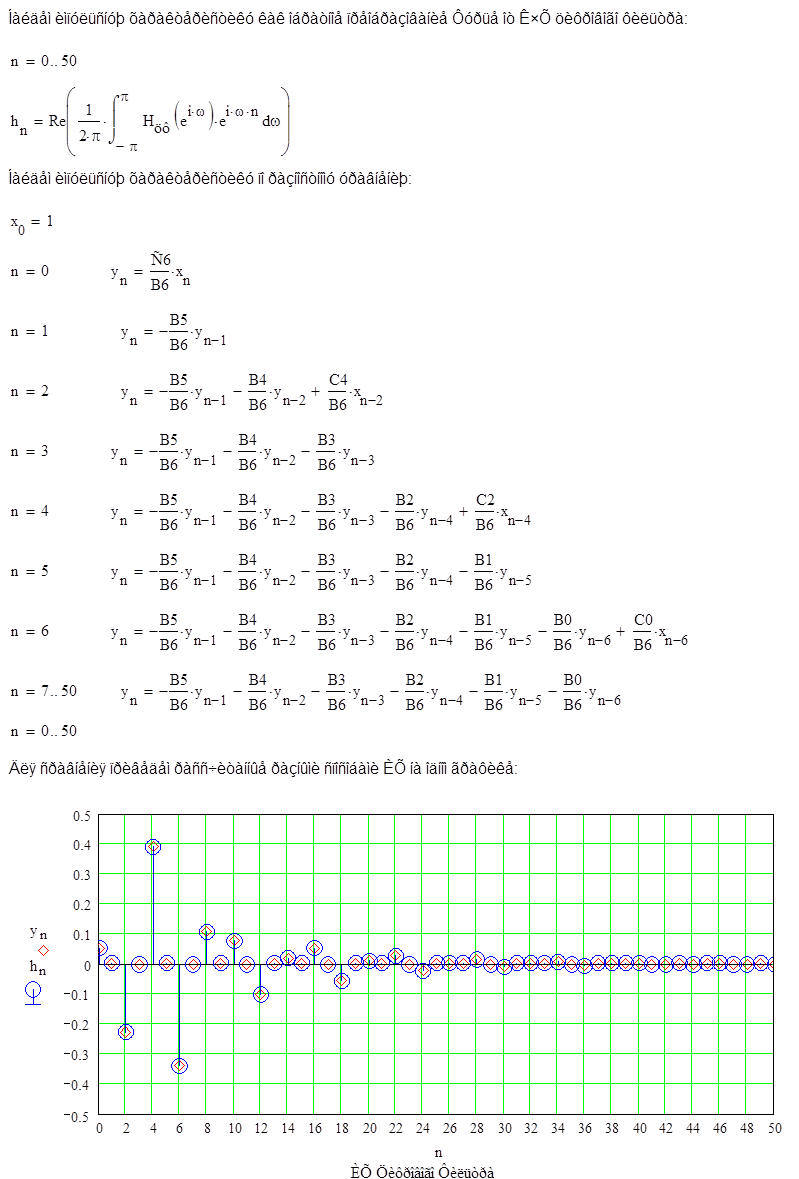
Видим, что ИХ найденные разными способами совпадают, что свидетельствует о правильности, проведенных преобразований.

Список литературы:

1.  Конспект лекций по Цифровой Обработке Сигналов.

2.  Введение в теорию ЦОС. В.Н. Васюков. Учебное пособие. Новосибирск, 1996.

3.  Методы ЦОС. В.Н. Васюков. Учебное пособие. Новосибирск, 1998.