Антенные фильтры, образованные ответвителями с параллельным соединением плеч. Антенные полосно-заграждающие фильтры на основе симметричных направленных ответвителей, страница 5

Эти свойства частотных характеристик антенных ПЗФ являются исходными при синтезе и позволяют рассчитать волновые сопротивления образующих его ступеней. Однако при синтезе рассматриваемого фильтра целесообразно отметить ряд ключевых особенностей, описанных в работе [58].

Прежде всего подчеркнем, что  при  формировании  числителя устойчивой передаточной функции  НО в терминах переменной Ричардса, когда решается характеристическое уравнение

   (3.17)

образуются две группы нулей. В первую группу объединяются комплексные корни (3.17), удовлетворяющие условию , во вторую – корни (3.17) с условием . После пересчета корней согласно тангенсному частотному преобразованию Ричардса  возможно следующее расположение на плоскости комплексной переменной  нулей  передаточной функции :

– квартеты (две комплексные сопряженные пары ), имеющие квадрантную симметрию, условие ;

– пары вещественных нулей , симметричных относительно мнимой оси , условие ;

– пары мнимых сопряженных нулей , условие ;

– один нуль в начале координат плоскости .

Что касается знаменателя  устойчивой передаточной функции, то ее полюса , т. е. корни характеристического уравнения

   (3.18)

образуют комплексные сопряженные пары с отрицательными вещественными частями  и один отрицательный вещественный полюс. В результате использования классической процедуры синтеза, описанной в работе [54] для ответвителей, с учетом вышеупомянутых особенностей находятся искомые значения волновых сопротивлений фильтра.

Рассчитаем антенный ПЗФ по варианту 1 при ,  дБ,  дБ. После подстановки  в формулы (3.15), (3.16) получаем

При этом коэффициенты  определялись стандартным методом Ньютона–Рафсона, подробно прокомментированным в работе [60] и справочниках по математике. Точность выбиралась такой, чтобы гарантировать шесть значащих цифр после запятой. Решение уравнений (3.17), (3.18) дает следующие значения нулей  и полюсов :

 После пересчета корней в числителе имеют место квартет   1.0642 0.7928 и нуль в начале координат, а в знаменателе – две комплексные сопряженные пары – 1.3168 0.6865, – 0.8916 0.6406 и вещественный полюс – 0.2522. В результате определяются волновые сопротивления ступеней синтезируемого фильтра:  ,  а затем – поперечные геометрические размеры их полосковых линий.

Линии реализованы согласно работе [20] с обеих сторон фольгированной диэлектрической пленки Ф4 МБСФ-2 толщиной 0,12 мм (рис. 3.11). Пленка со сформированными линиями помещена между двумя листами диэлектрика ФФ-4 толщиной 6 мм (образованными двумя более тонкими листами по 3 мм), после чего вся пятислойная структура уложена в герметичный корпус соответствующего типоразмера с коаксиально-полосковыми переходами СРГ-50-751ФВ. При этом геометрические размеры линий с волновым сопротивлением подводящих линий = 50 Ом составили (рис. 3.11):  = 8.5 мм;  = 2.5 мм;  = 7 мм;  = 0.3 мм; = 0.6 мм; ширина подводящих линий  = 10 мм. Такое выполнение фильтра обеспечивает минимально возможную электрическую длину  соединительного отрезка. Для перехода с одной стороны пленки на другую предусмотрено сквозное прямоугольное металлизированное отверстие (МО).

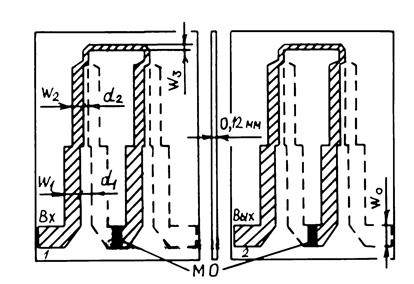
Рис. 3.11

Результаты измерений разработанного ПЗФ на панорамном измерителе параметров типа Р4-11 показали, что минимальное затухание в полосе заграждения составило 19 дБ на частоте последнего, самого высокочастотного минимума. Число всплесков затухания равно шести, их величина превышала предел измерений аппаратуры, равный 45 дБ. По сравнению с известным [56] фильтром описанная выше конструкция обеспечила при одинаковых уровнях  в 2.3 раза бльшую широкополосность диапазона заграждения гармоник.

Далее был реализован ПЗФ по варианту 3 с двумя пульсациями в полосе пропускания при   и с теми же уровнями   = = 0,8 дБ,  = 20 дБ затухания . Опуская промежуточные вычисления, приведем итоговые результаты синтеза фильтра:  = 1.1904,  = –5.8662, = 5.7813,  =  = 1.4022,  = = 1.0549, 1.4693. Конструктивно этот фильтр исполнен аналогично предыдущему, только с другими поперечными геометрическими размерами. Результаты его экспериментальных исследований также показали, что имеющиеся расхождения с теорией незначительны.