Антенные фильтры, образованные ответвителями с параллельным соединением плеч. Антенные полосно-заграждающие фильтры на основе симметричных направленных ответвителей, страница 4

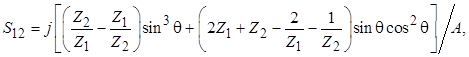
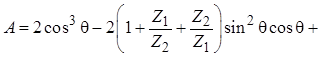               (3.9)

+

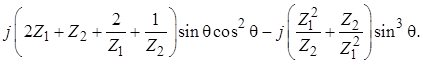
Здесь c целью сокращения записи сопротивления обозначены латинскими буквами:  электрическая длина отрезков;  соответственно текущая и центральная частоты рабочего диапазона ответвителя.

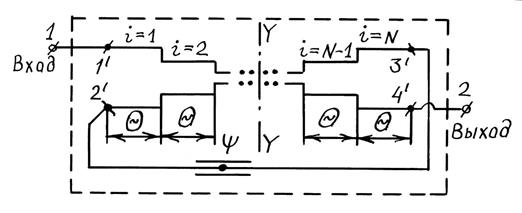
Рис. 3.8

Соединим плечи 2′ и 3′ НО отрезком линии передачи электрической длины , волновое сопротивление которой равно волновому сопротивлению тракта (рис. 3.8). Сформировавшийся четырехполюсник с номерами плеч 1 и 2 описывается матрицей рассеяния , элементы которой определяются с использо-ванием методики [51] применительно к восьмиполюснику 1′, 2′, 3′, 4′ с матрицей рассеяния (3.8):

         (3.10)

где

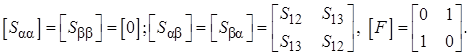(3.11)

Подстановка (3.11) в (3.10) приводит к результату

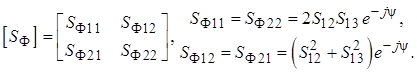     (3.12)

Форма частотных характеристик рабочего затухания позволяет отнести исследуемые четырехполюсники к классу полосно-заграждающих фильтров со всплесками затухания в полосе заграждения и пульсирующей или монотонной характеристикой в полосе пропускания. Число всплесков затухания и форма характеристики  в полосе пропускания зависят от величин волновых сопротивлений :

1) если ответвитель синтезирован по материалам работы [54] и имеет равнопульсирующее переходное затухание , то характеристика  будет монотонна в полосе пропускания при -м всплеске затухания в полосе заграждения (вариант 1);

2) если синтезируемый согласно [59] НО имеет максимально плоское затухание, то при монотонности характеристики  в полосе пропускания появляются лишь два всплеска затухания в полосе заграждения для любого  (вариант 2);

3) если ответвитель синтезирован так, что имеет всплески затухания  (например, по материалам работы [60]), то у фильтра появляются пульсации в полосе пропускания (вариант 3).

Так, например, на рис. 3.9 изображены частотные характеристики затухания ПЗФ с числом ступеней , рассчитанные по формулам (3.12), где сплошные линии относятся к варианту 1 при  штриховые – к варианту 2 при ; пунктирные – к варианту 3 при . Характеристики симметричны относительно вертикали в точке  и имеют в общем случае неоптимальную форму.

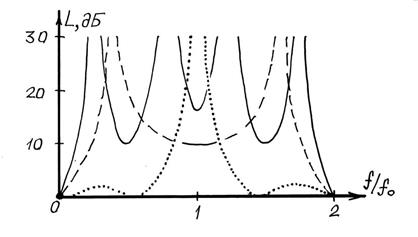
Рис. 3.9

На основании вышеописанного анализа можно потребовать, чтобы частотные характеристики затухания   антенных фильтров имели вид согласно рис. 3.10 (здесь для примера ), где – граница полосы пропускания в области нижних частот, отсчитываемая по уровню (дБ);  – нижняя граничная частота полосы заграждения по уровню (дБ). Верхняя граничная частота  полосы заграждения расположена симметрично относительно частоты  и на рис. 3.10 не показана. Для расчета оптимальных электрических параметров, в качестве которых будут выступать , целесообразно представить рабочее затухание  в форме

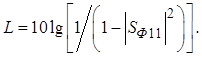                             (3.13)

Тогда на частотах минимумов затухания  в полосе заграждения с учетом реактивности ответвителя и унитарности его матрицы рассеяния  справедливо равенство

 (3.14)

а на частотах максимумов пульсаций  в полосе пропускания

               (3.15)

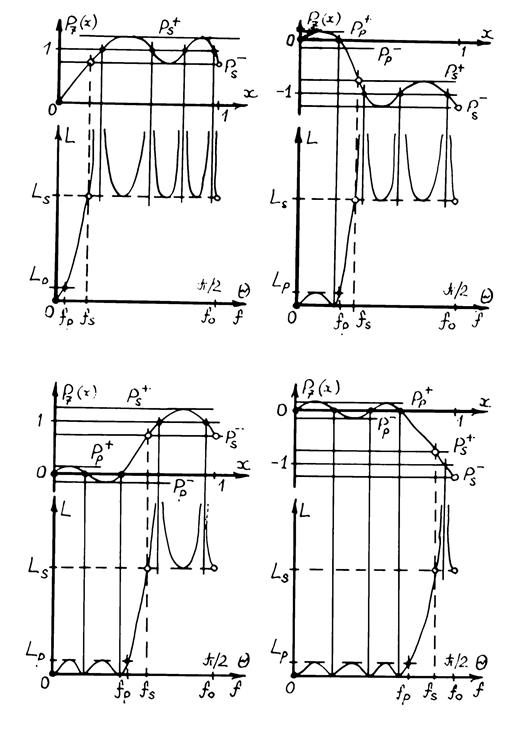
При этом следует учитывать номер варианта, по которому синтезируется фильтр. Так, на рис. 3.10 приведены частотные характеристики четырех фильтров, которые могут быть реализованы на основе 7-секционного () НО, причем рис. 3.10а соответствует варианту 1, а рис. 3.10б – г – варианту 3 с различным числом пульсаций в полосе пропускания. Частотные характеристики  однозначно определяют форму нечетного полинома седьмого порядка, используемого в классической процедуре синтеза симметричных НО [54, 59, 60] и имеющего экстремальные значения  в интервалах переменной , соответствующих полосам  пропускания  (индекс «»)  и заграждения (индекс «»):

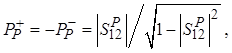
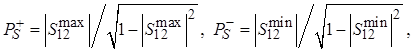
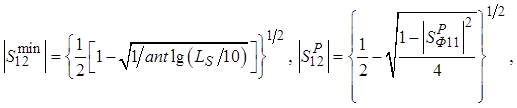
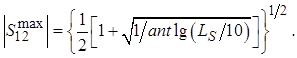                 (3.16)