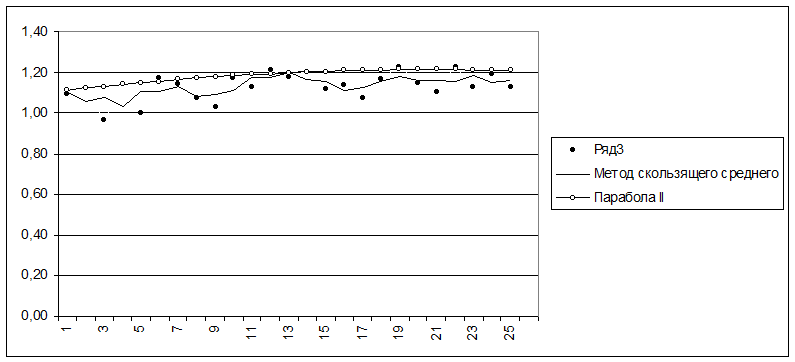
Для ряда 3:
|
Метод скользящего среднего |
Метод аналитического выравнивания |
||||
|
Линейная |
Лин.-гиперболическая |
Лин.-логарифмическая |
Парабола II |
Парабола III |
|
|
0,124569 |
1,165909 |
1,173266 |
1,163647 |
1,100211 |
1,133696 |
Среди рассмотренных альтернатив на роль функции тренда наилучшим образом подходит парабола II порядка:
f = 1,1+ 0,010941142622259 t – 0,000263572391485941 t2.
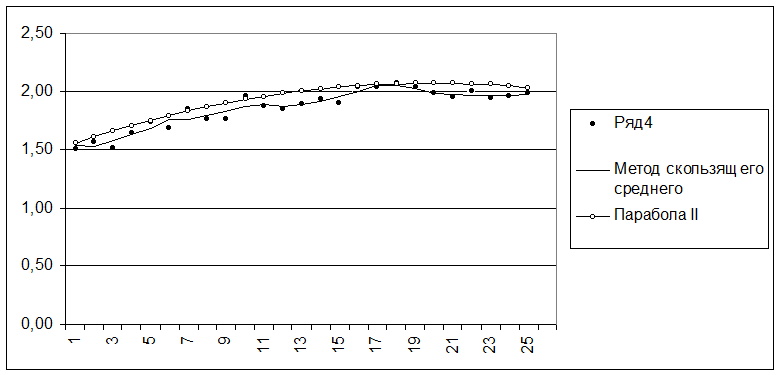
Для ряда 4:
|
Метод скользящего среднего |
Метод аналитического выравнивания |
||||
|
Линейная |
Лин.-гиперболическая |
Лин.-логарифмическая |
Парабола II |
Парабола III |
|
|
0,00184 |
2,562431 |
2,953579 |
2,113813 |
2,046911 |
2,088066 |
Среди рассмотренных альтернатив на роль функции тренда наилучшим образом подходит парабола II порядка:
f = 1,5+ 0,0573218668009327 t – 0,00144233036568111 t2.
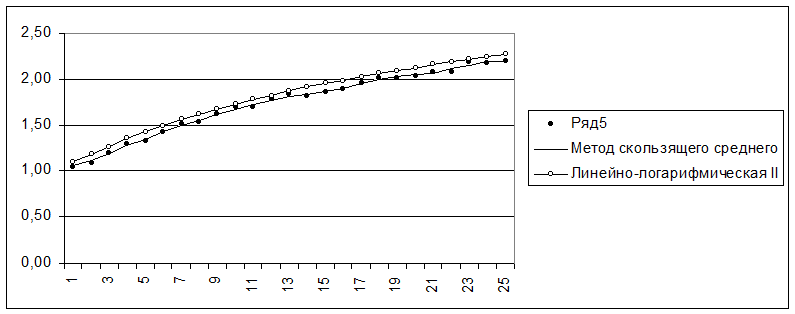
Для ряда 5:
|
Метод скользящего среднего |
Метод аналитического выравнивания |
||||
|
Линейная |
Лин.-гиперболическая |
Лин.-логарифмическая |
Парабола II |
Парабола III |
|
|
0,000339 |
1,271611 |
1,573349 |
0,705101 |
0,946456 |
0,840451 |
Среди рассмотренных альтернатив на роль функции тренда наилучшим образом подходит линейно-логарифмическая функция II порядка:
f = 1,1+ 0,0446117164986881 ln t + 0,0994168587124114 ln2 t.
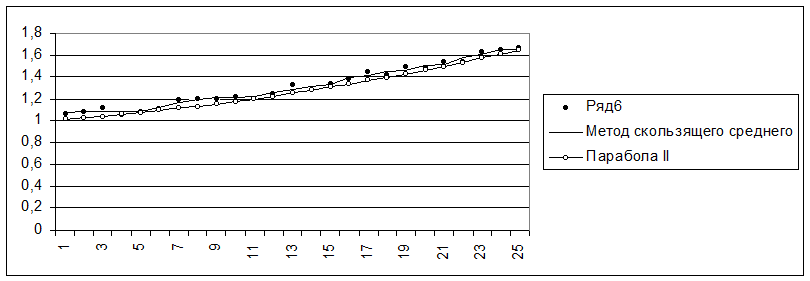
Для ряда 6:
|
Метод скользящего среднего |
Метод аналитического выравнивания |
||||
|
Линейная |
Лин.-гиперболическая |
Лин.-логарифмическая |
Парабола II |
Парабола III |
|
|
0,000554 |
0,951659 |
0,849397 |
1,263935 |
0,002153 |
1,113868 |
Среди рассмотренных альтернатив на роль функции тренда наилучшим образом подходит парабола II порядка:
f = 0,0122322710294178 t + 0,000539634932196183 t2.
Вывод: Качество аппроксимации наблюдений по методу скользящего среднего выше (ошибка во всех рассмотренных случаях меньше), чем при сглаживании методом аналитического выравнивания. Но метод скользящего среднего не позволяет вывести функциональную зависимость, характерную для данного ряда.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.