Производственная модель Леонтьева и основанные на ней методы оптимизации производственных процессов

Министерство Образования Российской Федерации

Новосибирский Государственный Технический Университет

Кафедра теории рынка

ЛАБОРАТОРНАЯ РАБОТА №3

ПРОИЗВОДСТВЕННАЯ МОДЕЛЬ ЛЕОНТЬЕВА

Вариант №3

Факультет:бизнеса

             Группа: ФБИ-93

Студенты: Бородихина И.А., Дашкова И.Ю., Дрегер Е.В.,

Птицына М.Н., Чепурная М.В.

Преподаватель:Фаддеенков А.В.

Новосибирск 

2002

Цель работы: ознакомиться с производственной моделью Леонтьева и основанными на ней методами оптимизации производственных процессов.

Матрица затрат:

продукт техн. процесс	G0	G1	G2
P1	0,1	0,5	0,6
P2	0,3	0,2	0,5
P3	0,2	0,4	0,1
P4	0,5	0,1	0,3

P₁, P₄ производят G₁. P₂, P₃ производят G₂, G₀ – труд.

Выполнение работы:

Задача анализа производственной модели Леонтьева основывается на теореме о замещении. При известных производительности технологических процессов и матрице затрат задачу минимизации затрат труда для реализации требуемого чистого выпуска и определения базиса модели можно сформулировать следующим образом:

                                  (6)

при ограничениях

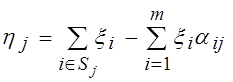, ,          (7)

где  – вектор затрат труда, требуемых для каждого технологического процесса;  – вектор интенсивностей использования технологических процессов;  – вектор чистого выпуска;  – множество технологических процессов, способных производить продукт ;  – объем затрат продукта  в технологическом процессе .

Задача (6),(7) является задачей линейного программирования, для ее решения можно воспользоваться, например, симплексным методом. Найденное решение позволит однозначно судить об оптимальном плане использования технологических процессов в модели – те компоненты вектора интенсивностей, которые не равны нулю, составляют базис (структуру) простой модели Леонтьева.

Простая модель Леонтьева:

0.1x₁+0.3x₂+0.2x₃+0.5x₄→ min

x₁+x₄ – (0.5x₁+0.2x₂+0.4x₃+0.1x₄) = 1

x₂+x₃ – (0.6x₁+0.5x₂+0.1x₃+0.3x₄) = 1

0.1x₁+0.3x₂+0.2x₃+0.5x₄→ min

x₁(1-0.5) – 0.2x₂ – 0.4x₃+x₄(1-0.1)=1

-0.6x₁+x₂(1-0.5)+x₃(1-0.1)-0.3x₄=1

0.1x₁+0.3x₂+0.2x₃+0.5x₄→ min

0.5x₁ – 0.2x₂ – 0.4x₃+0.9x₄=1

-0.6x₁+0.5x₂+0.9x₃ - 0.3x₄=1

При изменении вектора чистого выпуска , получаем различные векторы интенсивностей использования технологических процессов , используя ПЭР:

1.  при y = (1,1) x = (0;0;1.7391;1.8841).

+-----------------------------------------------------------------+

¦                  ИТОГОВЫЙ РЕЗУЛЬТАТ ДЛЯ lab3     Стр. : 1       ¦

¦-----------------------------------------------------------------¦

¦Переменн.¦          ¦Двойственн.¦Переменн.¦          ¦Двойственн.¦

¦No. Имена¦ РЕШЕНИЕ  ¦   оцен    ¦No. Имена¦ РЕШЕНИЕ  ¦   оцен    ¦

¦---------+----------+-----------+---------+----------+-----------¦

¦1   X1   ¦    0.0000¦    0.0609 ¦4   X4   ¦    1.8841¦    0.0000 ¦

¦2   X2   ¦    0.0000¦    0.1725 ¦5   A1   ¦    0.0000¦   -0.7391 ¦

¦3   X3   ¦    1.7391¦    0.0000 ¦6   A2   ¦    0.0000¦   -0.5507 ¦

¦-----------------------------------------------------------------¦

¦          MIN   величина цел.ф-и = 1.289855  Итерац.= 2          ¦

+-----------------------------------------------------------------+

2.  при y = (1,0) x = (0;0;0.4348;1.3043).

+-----------------------------------------------------------------+

¦                 ИТОГОВЫЙ РЕЗУЛЬТАТ ДЛЯ lab3      Стр. : 1       ¦

¦-----------------------------------------------------------------¦

¦Переменн.¦          ¦Двойственн.¦Переменн.¦          ¦Двойственн.¦

¦No. Имена¦ РЕШЕНИЕ  ¦   оцен    ¦No. Имена¦ РЕШЕНИЕ  ¦   оцен    ¦

¦---------+----------+-----------+---------+----------+-----------¦

¦1   X1   ¦    0.0000¦    0.0609 ¦4   X4   ¦    1.3043¦    0.0000 ¦

¦2   X2   ¦    0.0000¦    0.1725 ¦5   A1   ¦    0.0000¦   -0.7391 ¦

¦3   X3   ¦    0.4348¦    0.0000 ¦6   A2   ¦    0.0000¦   -0.5507 ¦

¦-----------------------------------------------------------------¦

¦          MIN   величина цел.ф-и = .7391305  Итерац.= 2          ¦

+-----------------------------------------------------------------+

3.  при y = (0,1) x = (0;0;1.3043;0.5797).

+-----------------------------------------------------------------+

¦                 ИТОГОВЫЙ РЕЗУЛЬТАТ ДЛЯ lab3      Стр. : 1       ¦

¦-----------------------------------------------------------------¦

¦Переменн.¦          ¦Двойственн.¦Переменн.¦          ¦Двойственн.¦

¦No. Имена¦ РЕШЕНИЕ  ¦   оцен    ¦No. Имена¦ РЕШЕНИЕ  ¦   оцен    ¦

¦---------+----------+-----------+---------+----------+-----------¦

¦1   X1   ¦    0.0000¦    0.0609 ¦4   X4   ¦    0.5797¦    0.0000 ¦

¦2   X2   ¦    0.0000¦    0.1725 ¦5   A1   ¦    0.0000¦   -0.7391 ¦

¦3   X3   ¦    1.3043¦    0.0000 ¦6   A2   ¦    0.0000¦   -0.5507 ¦

¦-----------------------------------------------------------------¦

¦          MIN   величина цел.ф-и = .5507247  Итерац.= 2          ¦

+-----------------------------------------------------------------+

Вывод: ознакомились с производственной моделью Леонтьева и основанными на ней методами оптимизации производственных процессов. Проанализировали изменение вектора интенсивностей использования технологических процессов при различных  векторах чистого выпуска.