Моментные функции. Стационарность и эргодичность.
Задан процесс Z(t):
1)
Определить математической ожидание 
,
дисперсию и корреляционную 
функцию процесса 
2)
Классифицировать процесс по признакам эргодичности и
стационарности
Где 
и
- детерминированные функции времени, описываемые
при помощи постоянных параметров 
и
X и Y -
некорреляррированные случайные величины с известными математическими ожиданиями
и 
и дисперсиями 
и
и автокорреляционные функции 
и
Исходные данные
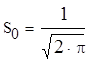
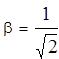
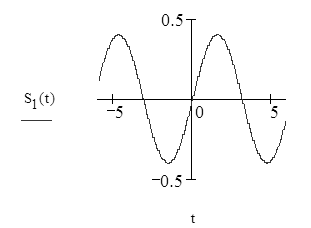
1. Определение Математического ожидания процесса
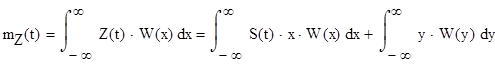
в силу неколляррированности величин X и Y в силу того что функция S(t) детерминированной, то есть конкретно определенная на каком-то интервале времени
2. Определение дисперсии процесса
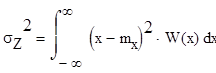
Так как величины X и Y некоррелированные случайные величины то пользуясь свойством дисперсии можно записать следующее
.
Так как
для некоррелированных величин выполняется равенство 
то
ковариация (из определения
некоррелярированных величин. Величины называются некоррелированными, если
выполняется равенство ) этих двух случайных величин
равна нулю. Процесс детерминированный то можно
записать следующее 
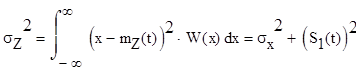
3. Определение корреляционной
функции
так как
не зависит от положения 
так как 
и
не зависят от положения то
в силу свойств математического ожидания и некоррелярированности величин
где 
4. Проверка на условие стационарности процесса
из данного выражение видно что математическое ожидание зависит от времени, то есть первое условие стационарности не выполняется
где
Второе условие стационарности то же не выполнено так как ковариационная функция зависит от положения времени отсчетов
Дальнейшая проверка необязательна так как первым двум из условий стационарности невыполнены то процесс нестационарен во времени.
Данный процесс на эргодичность можно не проверять так как не выполнено первые два условия стационарности то есть процесс не стационарен и некоррелирован.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
