Закон распределения (Экспоненциальный). Моментные функции. Стационарность и эргодичность

                        Министерство образования и науки Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

_____________________________________________________________________

Кафедра теоретических основ радиотехники (ТОР)

                    РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ

                                               ЗАДАНИЕ № 3

4.4.2. Закон распределения.

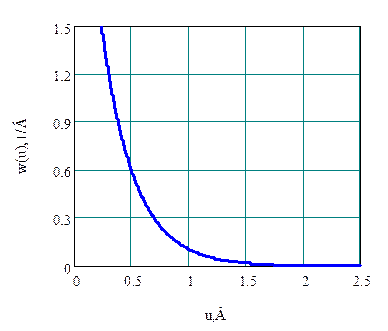
Задание. Стационарный случайный процесс U(t) описан плотностью вероятности W(u); параметры функции W(u) приведены ниже.

            Требуется:

1. Получить выражение для функции распределения F(u);
2. Построить график F(u);
3. Найти выражение для характеристической функции    и энтропии H.

Исходные данные

Закон распределения – Экспоненциальный

Аналитическая запись с помощью математического пакета Mathcad :         

Параметры:

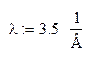
Плотность вероятности:

,

График плотности вероятности:

1. Нахождение выражения для функции распределения F(u).

 

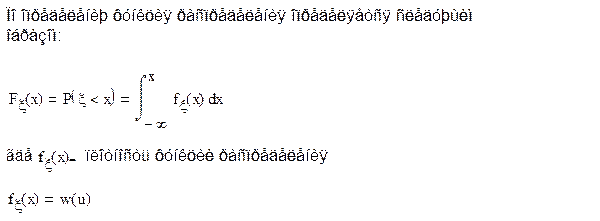
Формула из

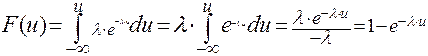
2. Построение графика функции распределения.

3. Нахождение выражения для характеристической функции Θ(ν)

По определению характеристическая функция определяется следующим образом:

Формула 4.2 из

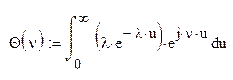
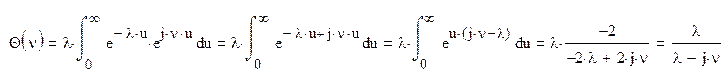
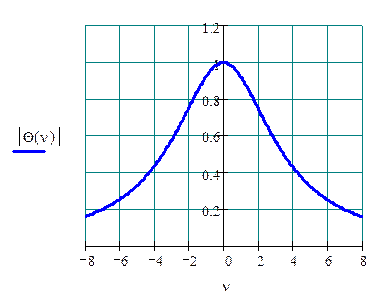
График характеристической функции:

4. Нахождение выражения для энтропии Н.

По определению (в общем случае) энтропия характеризует меру неопределенности системы.

Формула 4.11 из

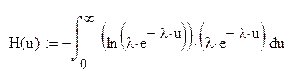
Искомая энтропия:

H = 0.25276

4.4.3. Моментные функции. Стационарность и эргодичность.

Задан процесс Z(t).

Требуется:

1. Определить математическое ожидание, дисперсию и корреляционную функцию Kz(t1,t2) процесса Z(t);
2. Классифицировать процесс Z(t) по признакам стационарности и эргодичности.

Где  и  - детерминированные функции времени, описываемые при помощи постоянных параметров  и

X и Y - некоррелированные случайные величины с известными математическими ожиданиями  и  и дисперсиями  и  , и автокорреляционными функциями  и  .

Исходные данные

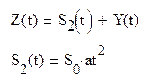
Определение математического ожидания:

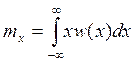
в силу некоррелированности величин  и  и в силу того, что функция  детерминирована (т.е. конкретно определена на каком-то интервале времени), а также в силу свойств математического ожидания получаем:

 (1)

Определение дисперсии:

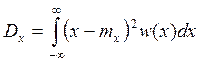
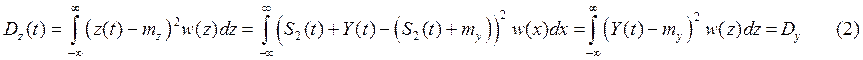
Определение корреляционной функции :

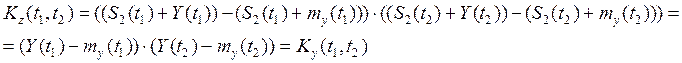
Проверка процесса на условие стационарности и эргодичности:

Процесс называется стационарным, если математическое ожидание и дисперсия не зависят от времени, а корреляционная функция зависит лишь от временного сдвига.

В нашем случае мы получили:

,

,

где m_y и D_y – математическое ожидание и дисперсия некоррелированной

случайной величины Y, не зависящие от времени;

то есть математическое ожидание процесса явно зависит от времени.

Полученная корреляционная функция процесса  также явно зависит от времени.

Итак, два условия стационарности процесса не выполнены, значит, исследуемый процесс нестационарен. Также процесс не является эргодическим, т.к. эргодический процесс – это разновидность стационарного процесса.

Список использованной литературы:

1.  Радиотехнические цепи и сигналы. Задачи и задания: Учеб. пособие / Коллектив авторов; под ред. проф. А.Н. Яковлева: Новосибирск, Изд-во НГТУ, 2002. – 348 с. (Серия «Учебники НГТУ»).

2.  Горяинов В.Т., Журавлев А.Г., Тихонов В.И. Статистическая радиотехника: Примеры и задачи. Учеб. пособие для вузов. – М.: Сов. радио, 1980. – 544 с.

3.  Гурский Е.И. Сборник задач по теории вероятностей и математической статистике. Минск, Издательство Вышэйшая школа, 1975.-272 с.

4.   Гоноровский И.С. Радиотехнические цепи и сигналы: Учебник. – М.:

Сов. радио, 1977. - 512 с

5.  В работе использованы формулы и некоторые данные из конспекта лекций  «Радиотехнические цепи и сигналы»