Спектральный анализ сигналов. Дискретизация непрерывных сигналов

2.4.1. Спектральный анализ сигналов

Требуется:

а) определить спектральную плостность S(f) сигнала S(t). Построить спектральные диаграммы модуля |S(f)| и фазы f(f), диаграмму энергитического спектра |S(f)|2;

б) найти ширину "лепестка" спектра одиночного импульса и сигнала;

в) вычислить энергию сигнала;

г) рассчитать коэффициенты Cn и Аn комплексного и тригонометрического ряда Фурье для периодического сигнала ST(t), полученного путем повторения заданного сигнала S(t) с периодом Tn . Построить соответствующие спектральные диаграммы |Cn|, Fn

è |An|,fn .

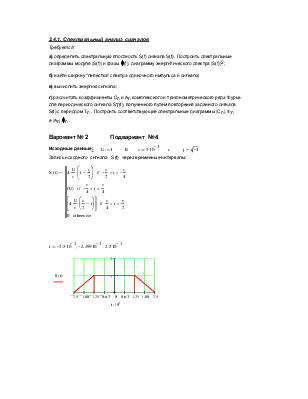
Вароиант № 2              Подвариант  № 4

Исходные данные:

Запись исходного  сигнала   S(t)  через временные интервалы:

Решение:

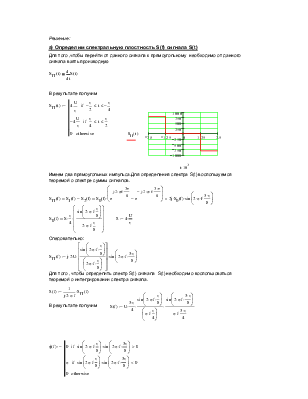
а) Определим спектральную плостность S(f) сигнала S(t)

Для того ,чтобы перейти от данного сигнала к прямоугольному  необходимо от данного сигнала взять производную

В результате получим

Имеем два прямоугольных импульса.Для определения спектра S(t) воспользуемся теоремой о спектре суммы сигналов.

Следовательно:

Для того , чтобы определить спектр S(t) сигнала  S(t) необходимо воспользоваться теоремой о интегрировании спектра сигнала.

В результате получим

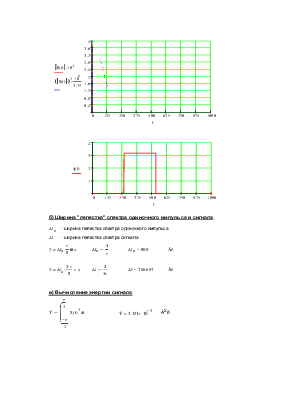
б) Ширина "лепестка" спектра одиночного импульса и сигнала

- ширина лепестка спектра одиночного импульса

- ширина лепестка спектра сигнала

в) Вычисление энергии сигнала

Â2ñ

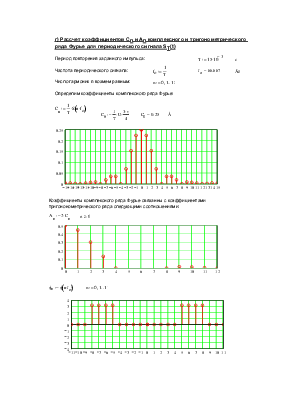
г) Рассчет коэффициентов Cn и Аn комплексного и тригонометрического ряда Фурье для периодического сигнала ST(t)

Период повторения заданного импульса:

Частота периодического сигнала:

Число гармоник n возмем равным:

Определим коэффициенты комплексного ряда Фурье:

Коэффициенты комплексного ряда Фурье связанны с коэффициентами тригононометрического ряда следующими соотношениями:

2.4.3. Дискритизация непрерывных сигналов

Требуется:

а) вычислить максимальную частоту fmax в спектре сигнала;

б) определить интервал дискретизации;

в) построить графики дискретизированного сигнала, если за дискретизирующую систему функций принять последовательность дельта-импульсов d(t);

г) определить спектр SD(f) дискетизированного в соответствии с п."3" сигнала.     Построить диаграмму спектральной плотности |SD(f)|.

Решение:

а) Максимальная частотя fmax в спектре сигнала;

За максимальную частоту fmax в спектре сигнала можно принять ширену первого "лепестка". Она будет равна:

б) Интервал дискретизации;

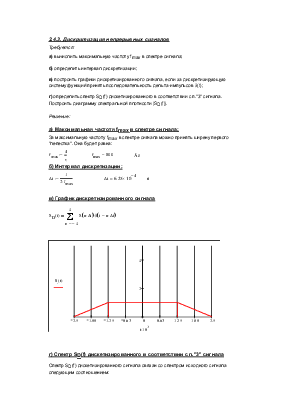
в) График дискретизированного сигнала

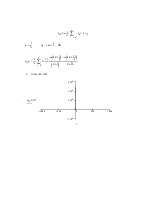
г) Спектр SD(f) дискетизированного в соответствии с п."3" сигнала

Спектр SD(f) дискетизированного сигнала связан со спектром исходного сигнала следующим соотношением:

Ãö