Министерство образования Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
_____________________________________________________________________
Кафедра теоретических
основ радиотехники (ТОР)
РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ
ЗАДАНИЕ № 1
СПЕКТРАЛЬНЫЙ СОСТАВ ТОКА В НЕЛИНЕЙНОМ ЭЛЕМЕНТЕ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ
ВОЗДЕЙСТВИЕ СТАЦИОНАРНОГО СЛУЧАЙНОГО ПРОЦЕССА НА БЕЗЫНЕРЦИОННЫЙ НЕЛИНЕЙНЫЙ ЭЛЕМЕНТ
Вариант № 4
Подвариант № 5
Факультет: РЭФ
Группа: РТ5-24
Студент: Никитин С.В.
Дата сдачи «24» сентября 2004 г.
Преподаватель: проф. Яковлев А.Н.
Новосибирск, 2004
1. Спектральный состав тока в нелинейном элементе при гармоническом воздействии.
Заданы
вольт-амперная характеристика безынерционного нелинейного элемента и вид
аппроксимирующей функции этой характеристики. На вход НЭ подано напряжение ![]() .
.
Требуется:
а) изобразить графически заданную ВАХ НЭ;
б) определить коэффициенты аппроксимирующей функции;
в) сравнить аппроксимированную характеристику с заданной, построив их на одном графике;
г) изобразить на одном графике временные диаграммы входного напряжения и тока через НЭ;
д)
найти спектральный состав тока НЭ: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
е) построить спектральные диаграммы входного напряжения и тока через НЭ.
Дано:
|
|
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
|
|
0 |
1.0 |
2.5 |
5.5 |
12 |
27 |
61 |
135 |
Аппроксимирующая
функция: ![]()
![]()
![]()
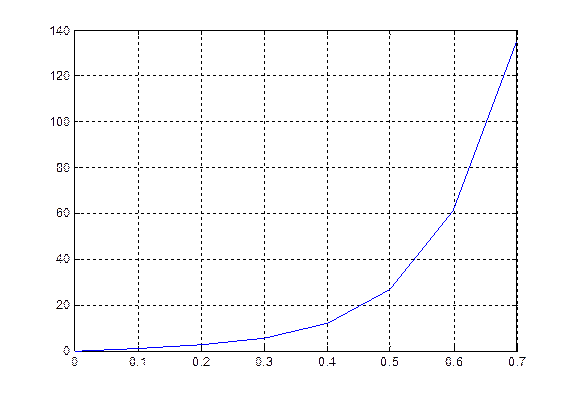
Графически изобразим ВАХ НЭ.
|
|
|
|
|
|
|
|
|
|
На графике (см. выше) непрерывной линией обозначена ВАХ, построенная при помощи линейной интерполяции. Функция int(x) – ВАХ НЭ, построенная при помощи кубической сплайн-интерполяции (вычисления проводились в среде MathCad 11).
u=[0 0.1 0.2 0.3 0.4 0.5 0.6 0.7];
i=[0 1.0 2.5 5.5 12 27 61 135];
plot(u,i);
grid on
Выше написано содержимое m-файла для создания графика ВАХ НЭ (линейная интерполяция по точкам) в среде MATLAB 6.5.
Определим коэффициенты аппроксимирующей функции.
Чтобы
определить коэффициент ![]() «сдвинем» график ВАХ влево на
значение равное
«сдвинем» график ВАХ влево на
значение равное ![]() .
.
|
|
|
|
|
|
Для определения коэффициента ![]() воспользуемся методом приведения к
линейному виду, заодно определим область справедливости аппроксимации.
воспользуемся методом приведения к
линейному виду, заодно определим область справедливости аппроксимации.
![]() -для
«сдвинутого» графика, где
-для
«сдвинутого» графика, где ![]() .
.
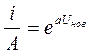 ;
; 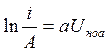 ;
; 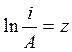 ;
; ![]()
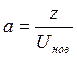 .
.
|
|
|
|
|
|
|
|
|
|
|
|
Матрицы ![]() и
и ![]() заданы
выше. Из графика видно, что коэффициент
заданы
выше. Из графика видно, что коэффициент ![]() можно
принять равным 7.95.
можно
принять равным 7.95.
Также видно, что аппроксимация справедлива с индекса 2 по индекс 5, что соответствует интервалу [0.3; 0.7].
Сравним аппроксимированную характеристику с заданной.
|
|
|
|
U0=0.275;
A=4.535;
u=[0 0.1 0.2 0.3 0.4 0.5 0.6 0.7];
i=[0 1.0 2.5 5.5 12 27 61 135];
z(k)=log(i(k)/A);
a(k)=z(k)./(u(k)-U0);
a
k=1:8;
plot(k,a,'-o');
grid on
ae=7.95;
x=0:0.02:0.7;
apr=A*exp(ae*(x-U0));
figure
plot(x,apr,u,i,':');
grid on
Выше приведено содержимое m-файла
для нахождения коэффициента ![]() и построения графиков
аппроксимированной и исходной функций, а также зависимости
и построения графиков
аппроксимированной и исходной функций, а также зависимости ![]() от индекса (результаты см. ниже) (среда MATLAB 6.5).
от индекса (результаты см. ниже) (среда MATLAB 6.5).
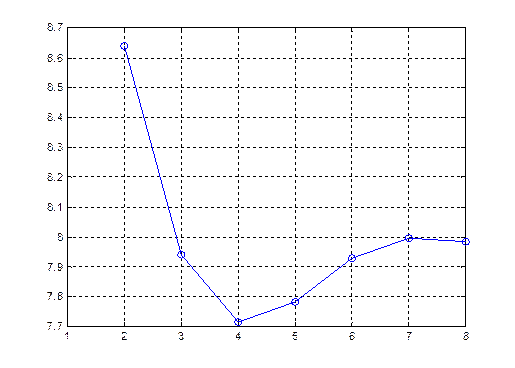
зависимость
коэффициента ![]() от
индекса
от
индекса
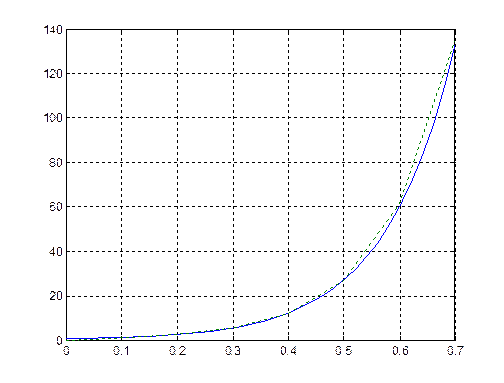
сравнение графиков исходной и аппроксимированной функций
Изобразим на одном графике временные диаграммы входного тока и напряжения через НЭ.
|
|
U0=0.275;
Um=0.175;
A=4.535;
ae=7.95;
t=0:0.0002:0.3;
uvh=U0+Um*cos(100*t);
iNE=A*exp(ae*(uvh-U0));
plot(t,iNE,t,20*uvh,'--');
grid on
Выше приведено содержание m-файла для построения графиков входного воздействия и тока через НЭ в среде MATLAB 6.5.
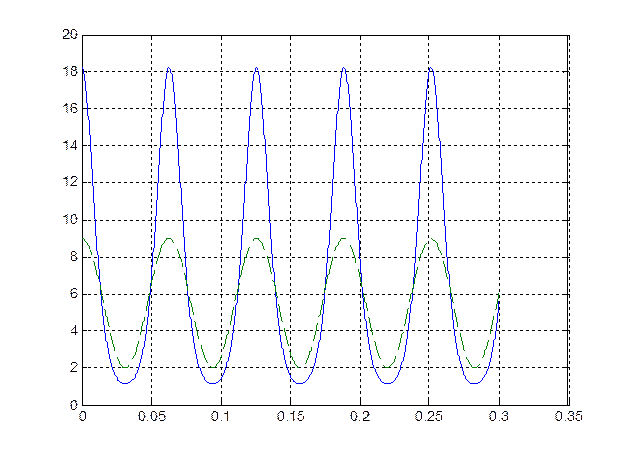
графики тока через НЭ (сплошная линия) и входного воздействия (штриховая линия)
Найдем спектральный
состав тока НЭ: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() , где
, где ![]() - ток в
рабочей точке.
- ток в
рабочей точке.
|
|
|
|
|
|
|
|
|
|
|
|
In – значения модифицированных функций Бесселя в точке ![]()
![]() .
.
Ampln – амплитуды спектральных составляющих в вольтах.
|
|
n – номера гармоник.
|
|
На левом графике – спектр тока через НЭ, на правом – спектр входного напряжения.
2. Воздействие стационарного случайного процесса на безынерционный нелинейный элемент.
На вход нелинейного
безынерционного элемента действует случайный процесс ![]() с
одномерной плотностью вероятности
с
одномерной плотностью вероятности ![]() . Характеристика НЭ, вид
аппроксимирующей функции и смещение такие же, что и в предыдущем задании.
Среднеквадратическое значение напряжения
. Характеристика НЭ, вид
аппроксимирующей функции и смещение такие же, что и в предыдущем задании.
Среднеквадратическое значение напряжения ![]() . Закон
распределения вероятностей входного случайного процесса:
. Закон
распределения вероятностей входного случайного процесса: 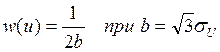 .
.
Требуется:
а) определить одномерную
плотность вероятности ![]() на выходе НЭ;
на выходе НЭ;
б) построить графики ![]() и
и ![]() ;
;
в) найти математическое
ожидание ![]() , дисперсию
, дисперсию ![]() и
среднюю мощность
и
среднюю мощность ![]() случайного процесса на выходе
безынерционного НЭ.
случайного процесса на выходе
безынерционного НЭ.
1) определим одномерную
плотность вероятности ![]() на выходе НЭ;
на выходе НЭ;
![]()
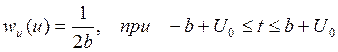
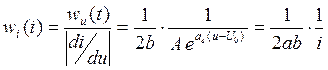
2) построим графики ![]() и
и ![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) найдем математическое
ожидание ![]() , дисперсию
, дисперсию ![]() и
среднюю мощность
и
среднюю мощность ![]() случайного процесса на выходе
безынерционного НЭ.
случайного процесса на выходе
безынерционного НЭ.
|
|
|
|
|
|
|
|
|
|
|
|
Um=0.175;
U0=0.275;
sigmau=Um;
b=sqrt(3)*sigmau;
t1=-0.4:0.001:-b+U0;
t2=-b+U0:0.001:b+U0;
t3=b+U0:0.001:1;
wu1=0.*t1;
wu2=((1/(2*b)).*t2)./t2;
wu3=0.*t3;
wu=[wu1 wu2 wu3];
t=[t1 t2 t3];
plot(t,wu);
grid on
A=4.535;
ae=7.95;
imin=A*exp(ae*(-b+U0-U0));
imax=A*exp(ae*(b+U0-U0));
z1=-5:imin/100:imin;
z2=imin:(imax-imin)/100:imax;
z3=imax:0.01:52;
wi1=0.*z1;
wi2=(1/(2*ae*b))./z2;
wi3=0.*z3;
z=[z1 z2 z3];
wi=[wi1 wi2 wi3];
figure
plot(z,wi);
grid on
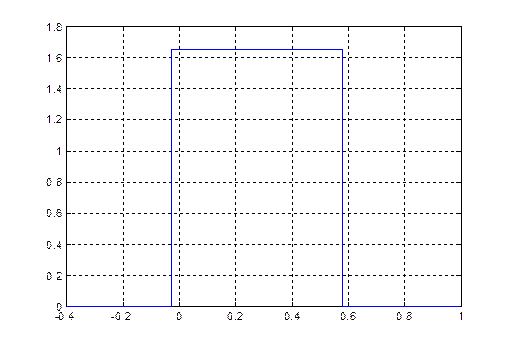
график функции распределения входного сигнала
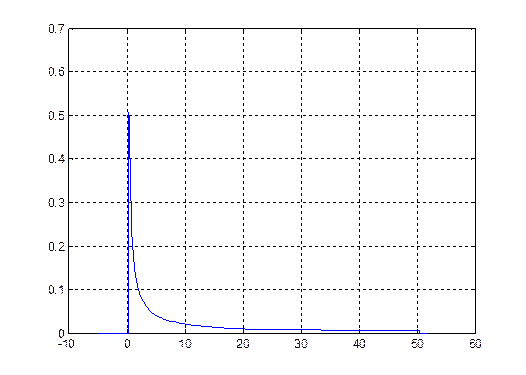
график функции распределения тока через НЭ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.