Министерство образования и науки Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
_____________________________________________________________________
Кафедра теоретических
основ радиотехники (ТОР)
РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ
ЗАДАНИЕ N 3
Закон распределения
Моментные функции. Стационарность и эргодичность
Вариант N 4
Подвариант N 0
Факультет РЭФ
Группа РТ- 5 -81
Студент: Любимов И.К.
Дата сдачи « » май 2010 г.
Преподаватель: проф. Яковлев А.Н.
Новосибирск, 2010
Закон распределения
Стационарный случайный
процесс ![]() описан плотностью вероятности
описан плотностью вероятности ![]()
Требуется:
а) получить выражение для функции
распределения ![]() ;
;
б) построить график ![]() ;
;
в) найти выражение для
характеристической функции ![]() и энтропии Н.
и энтропии Н.
Закон распределения --- Релея
Плотность вероятности ![]() Аналитическая запись
Аналитическая запись 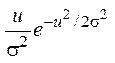 ,
,![]()
График 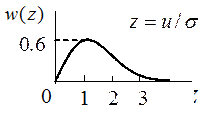
|
|
Выражение для функции распределения выглядит:
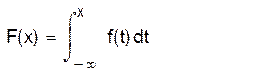 где
где
![]() плотность функции распределения
плотность функции распределения ![]()
Получаем что при u<=0
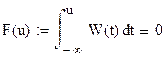 а при u>0
а при u>0
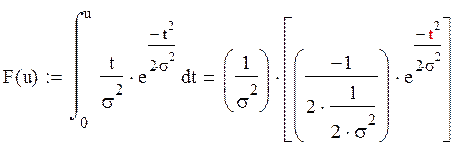
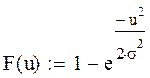
График данной функции имеет вид:
|
|
По определению характеристическая функция определяется как:
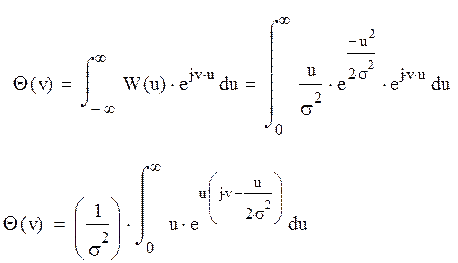
Запишем выражение для энтропии
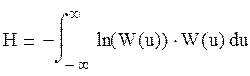
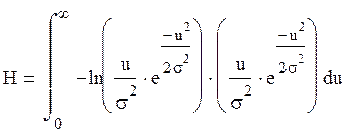
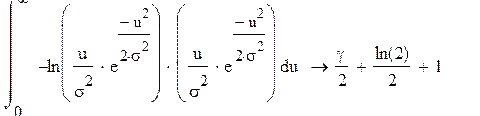
Моментные функции. Стационарность и эргодичность
![]() и
и ![]() –
детерминированные функции времени, описываемые с помощью постоянных параметров
–
детерминированные функции времени, описываемые с помощью постоянных параметров ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]()
Требуется:
а) определить математическое ожидание ![]() ,
дисперсию
,
дисперсию ![]() и корреляционную функцию
и корреляционную функцию![]() процесса
процесса ![]() ;
;
б) классифицировать процесс ![]() по
признакам стационарности и эргодичности.
по
признакам стационарности и эргодичности.
![]() и
и ![]() –
некоррелированные эргодические случайные процессы, которые соответственно имеют
известные математические ожидания
–
некоррелированные эргодические случайные процессы, которые соответственно имеют
известные математические ожидания ![]() и
и ![]() дисперсии
дисперсии ![]() и
и ![]() и автокорреляционные функции
и автокорреляционные функции ![]() и
и ![]() .
.
![]() и
и ![]() –
некоррелированные случайные величины с известными математическими ожиданиями
–
некоррелированные случайные величины с известными математическими ожиданиями ![]() и
и ![]() и
дисперсиями
и
дисперсиями ![]() и
и ![]() ;
;
Дано:
![]()
![]()
РЕШЕНИЕ
Определим математическое ожидания
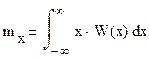 тогда
тогда
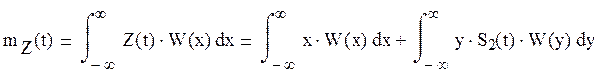
В силу некоррелированности случайной величины Х и S(t) детерминированная функция получим
![]()
Определение дисперсии
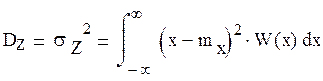
Так как величины Х и Y случайные некоррелированные величины то, пользуясь свойством дисперсии можно записать:
![]()
из теории вероятности: по теореме о необходимом условии независимости случайных величин, получим при независимости X и Y
![]()
Учитывая тот факт что S2(t) детерминированный то выражения для дисперсии примет вид:
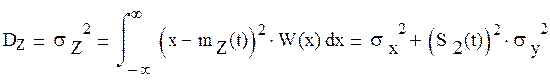
Определение корреляционной функции ![]()
![]()
в силу свойств математического ожидания и некоррелированности величин
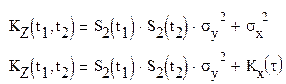 где
где ![]()
Проверим условие стационарности процесса
![]()
из данного равенства находится, что математическое ожидание зависит от времени, следовательно первое условие стационарности не выполняется.
![]()
Второе условие так же не выполнено, так как ковариационная
функция зависит от положения времени отсчетов, а не только от ![]()
В связи с не выполнениями условий, процесс нельзя считать стационарным, а так же эргодическим и некоррелированным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.