






Министерство образования и науки Российской Федерации
Новосибирский государственный технический университет
Кафедра РП и РПУ
Лабораторная работа №3 по курсу
«Радиоавтоматика».
Тема: Исследование нелинейных систем автоматического регулирования
Факультет: РЭФ
Группа: РТВ14-92
Студент: Шатров М.С.
Преподаватель: Лявданский С.Е.
Новосибирск 2012
Цель работы: исследовать свойства нелинейных систем (устойчивости и формы импульсной характеристики) нескольких структур нелинейных систем, а именно:
- два варианта линейной части системы: статическая из трёх инерционных звеньев, а также астатическая из одного интегрирующего и двух инерционных звеньев;
- три варианта нелинейностей с каждой из вышеупомянутых линейных частей: нелинейности «насыщение», «зона нечувствительности», «зона нечувствительности с насыщением».
Результаты исследования.
Структурная схема системы:
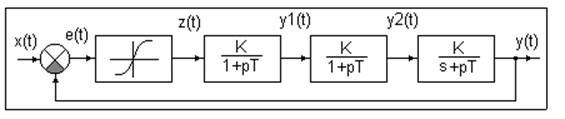
При s=1 – система статическая, при s=0 – система астатическая 1-го порядка.
Задание входного сигнала:
Входной сигнал представлен функцией единичного импульсного воздействия (функция Дирака).
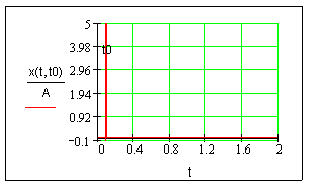
1.1. Рассмотрим случай, при котором линейное звено представлено тремя инерционными звеньями, а нелинейность - «насыщение». Система является статической, устойчивой. Передаточные функции линейного звена системы описывается выражением:
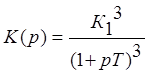
Характеристика нелинейного элемента и годограф линейного звена представлены на рисунках:
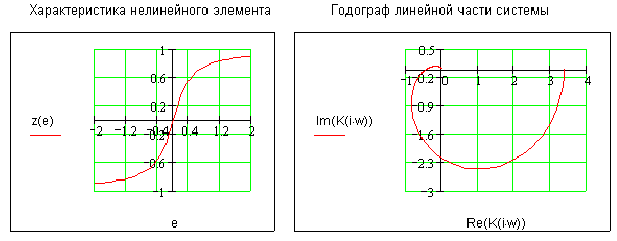
Данная нелинейная система описывается фазовым портретом и следующей диаграммой Гольдфарба:
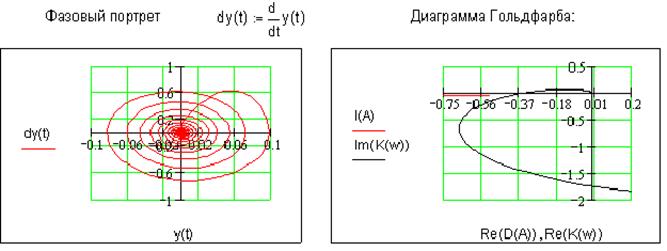
Судя
по диаграмме Гольдфарба данная система является устойчивой, так как годограф
функции, обратной коэффициенту передачи нелинейного звена как функция амплитуды
![]() и годограф линейного звена
и годограф линейного звена ![]() не пересекаются. При заданном коэффициенте
усиления линейного звена автоколебания невозможны, однако с увеличением
коэффициента усиления годографы линейной и нелинейной части пересекаются. Это
можно проследить на следующем примере, при котором
не пересекаются. При заданном коэффициенте
усиления линейного звена автоколебания невозможны, однако с увеличением
коэффициента усиления годографы линейной и нелинейной части пересекаются. Это
можно проследить на следующем примере, при котором ![]() . Для системы с
коэффициентом усиления линейной системы
. Для системы с
коэффициентом усиления линейной системы ![]() диаграмма
Гольдфарба выглядит следующим образом:
диаграмма
Гольдфарба выглядит следующим образом:
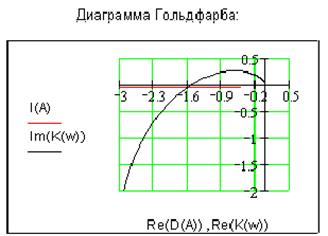
В такой системе возможны автоколебания
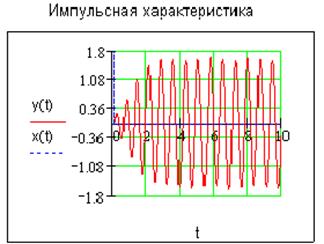
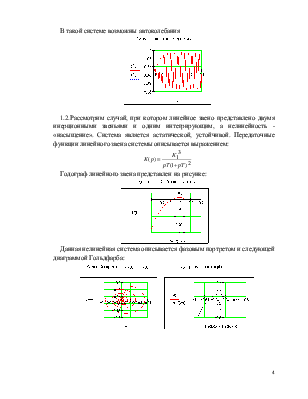
1.2. Рассмотрим случай, при котором линейное звено представлено двумя инерционными звеньями и одним интегрирующим, а нелинейность - «насыщение». Система является астатической, устойчивой. Передаточные функции линейного звена системы описывается выражением:
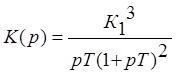
Годограф линейного звена представлен на рисунке:
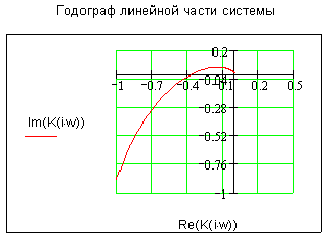
Данная нелинейная система описывается фазовым портретом и следующей диаграммой Гольдфарба:
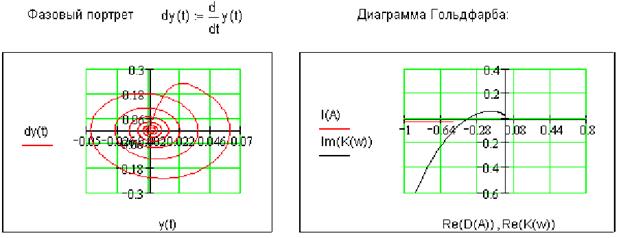
Судя
по диаграмме Гольдфарба данная система является устойчивой, так как годограф
функции, обратной коэффициенту передачи нелинейного звена как функция амплитуды
![]() и годограф линейного звена
и годограф линейного звена ![]() не пересекаются. При заданном коэффициенте
усиления линейного звена автоколебания невозможны, однако с увеличением
коэффициента усиления годографы линейной и нелинейной части пересекаются. Это
можно проследить на следующем примере, при котором
не пересекаются. При заданном коэффициенте
усиления линейного звена автоколебания невозможны, однако с увеличением
коэффициента усиления годографы линейной и нелинейной части пересекаются. Это
можно проследить на следующем примере, при котором ![]() . Для системы с
коэффициентом усиления линейной системы
. Для системы с
коэффициентом усиления линейной системы ![]() диаграмма
Гольдфарба выглядит следующим образом:
диаграмма
Гольдфарба выглядит следующим образом:
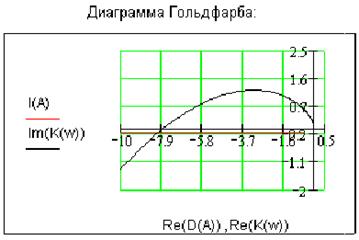
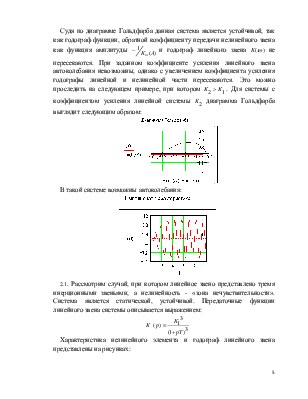
В такой системе возможны автоколебания:
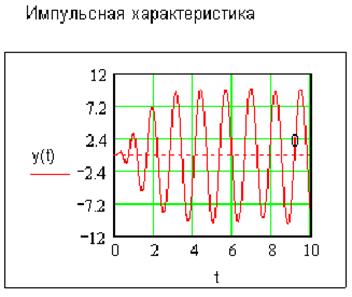
2.1. Рассмотрим случай, при котором линейное звено представлено тремя инерционными звеньями, а нелинейность - «зона нечувствительности». Система является статической, устойчивой. Передаточные функции линейного звена системы описывается выражением:
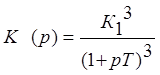
Характеристика нелинейного элемента и годограф линейного звена представлены на рисунках:
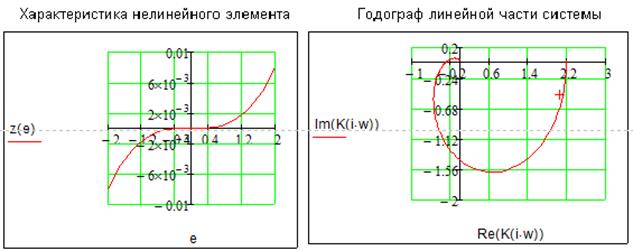
Данная нелинейная система описывается фазовым портретом и следующей диаграммой Гольдфарба:
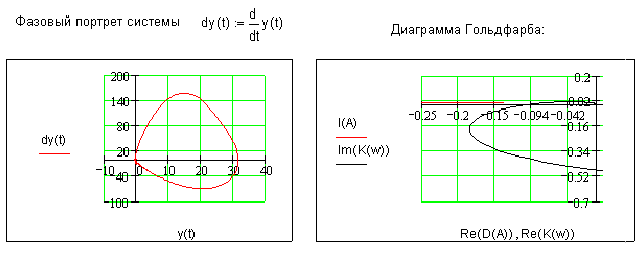
Судя
по диаграмме Гольдфарба данная система является устойчивой, так как годограф
функции, обратной коэффициенту передачи нелинейного звена как функция амплитуды
![]() и годограф линейного звена
и годограф линейного звена ![]() не пересекаются. При заданном коэффициенте
усиления линейного звена автоколебания невозможны. С увеличением коэффициента
усиления годографы линейной и нелинейной части пересекаются. Это можно
проследить на следующем примере, при котором
не пересекаются. При заданном коэффициенте
усиления линейного звена автоколебания невозможны. С увеличением коэффициента
усиления годографы линейной и нелинейной части пересекаются. Это можно
проследить на следующем примере, при котором ![]() . Для системы с
коэффициентом усиления линейной системы
. Для системы с
коэффициентом усиления линейной системы ![]() диаграмма
Гольдфарба выглядит следующим образом:
диаграмма
Гольдфарба выглядит следующим образом:
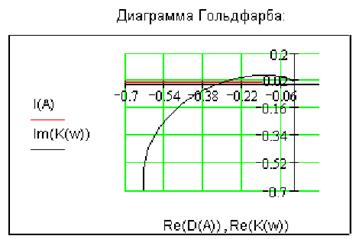
В такой системе возможны автоколебания:
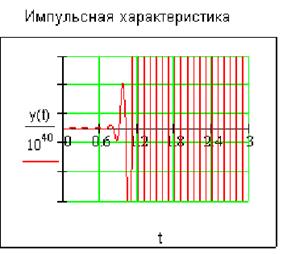
2.2. Рассмотрим случай, когда система является астатической, устойчивой. Передаточные функции линейного звена системы описывается выражением:
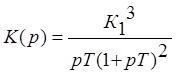
Годограф линейного звена представлен на рисунке:
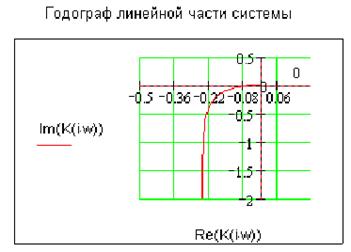
Данная нелинейная система описывается фазовым портретом и следующей диаграммой Гольдфарба:
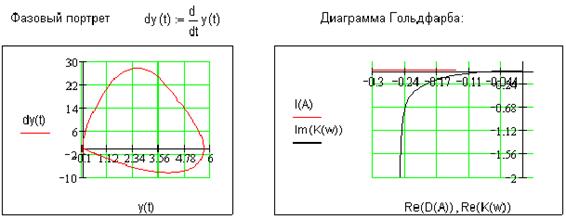
Судя по
диаграмме Гольдфарба данная система является устойчивой, так как годограф
функции, обратной коэффициенту передачи нелинейного звена как функция амплитуды
![]() и годограф линейного звена
и годограф линейного звена ![]() не пересекаются. При заданном коэффициенте
усиления линейного звена автоколебания невозможны, однако с увеличением
коэффициента усиления годографы линейной и нелинейной части пересекаются. Это
можно проследить на следующем примере, при котором
не пересекаются. При заданном коэффициенте
усиления линейного звена автоколебания невозможны, однако с увеличением
коэффициента усиления годографы линейной и нелинейной части пересекаются. Это
можно проследить на следующем примере, при котором ![]() .
.
Для системы с
коэффициентом усиления линейной системы ![]() диаграмма
Гольдфарба выглядит следующим образом:
диаграмма
Гольдфарба выглядит следующим образом:
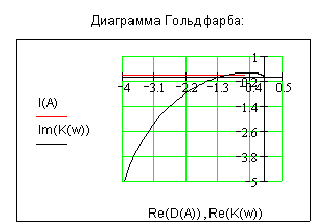
В такой системе возможны автоколебания:
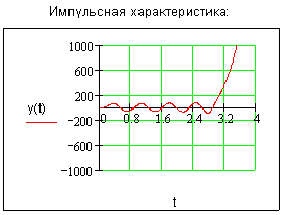
3.1. Рассмотрим случай, при котором линейное звено представлено тремя инерционными звеньями, а нелинейность - «нечувствительность с насыщением». Система является статической. Передаточные функции линейного звена системы описывается выражением:
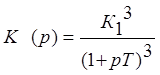
Характеристика нелинейного элемента и годограф линейного звена представлены на рисунках:
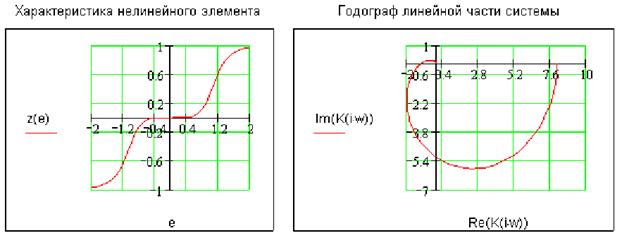
Данная нелинейная система описывается фазовым портретом и следующей диаграммой Гольдфарба:
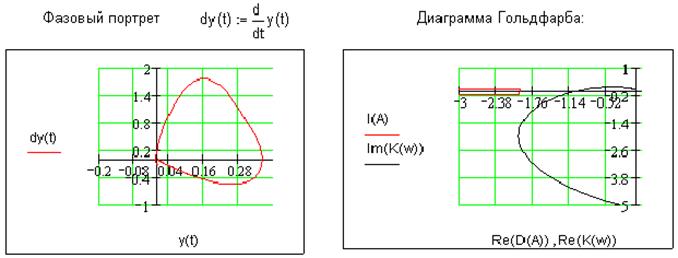
Судя по
диаграмме Гольдфарба данная система является устойчивой, так как годограф
функции, обратной коэффициенту передачи нелинейного звена как функция амплитуды
![]() и годограф линейного звена
и годограф линейного звена ![]() не пересекаются. При заданном коэффициенте
усиления линейного звена автоколебания невозможны, однако с увеличением
коэффициента усиления годографы линейной и нелинейной части пересекаются. Это
можно проследить на следующем примере, при котором
не пересекаются. При заданном коэффициенте
усиления линейного звена автоколебания невозможны, однако с увеличением
коэффициента усиления годографы линейной и нелинейной части пересекаются. Это
можно проследить на следующем примере, при котором ![]() . Для системы с коэффициентом усиления
линейной системы
. Для системы с коэффициентом усиления
линейной системы ![]() диаграмма Гольдфарба выглядит следующим
образом:
диаграмма Гольдфарба выглядит следующим
образом:
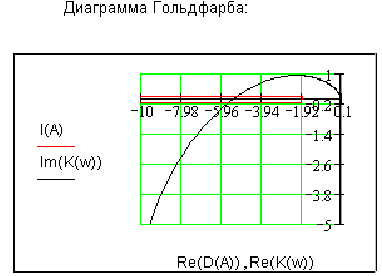
Данная система имеет своеобразный вид – годограф нелинейного звена состоит из двух составляющих. В первом случае годограф входит в область годографа линейной части системы, и, не смотря на пересечение годографов, автоколебания будут неустойчивы, то есть, практически их нельзя будет наблюдать. Во втором случае автоколебания будут устойчивы в точке пересечения годографов, так как при приращении аргумента А на годографе нелинейной части он выходит из пределов комплексной плоскости, очерченных годографом линейной части.
Фазовый портрет такой системы представлен на следующем рисунке:
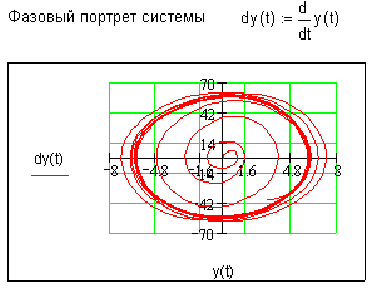
Вывод:
1. Если годографы по диаграмме Гольдфарба не пересекаются, то нелинейная система абсолютно устойчива и в ней не могут существовать автоколебания.
2. Если годографы пересекаются, то такая система является неустойчивой и в ней возможны автоколебания. Они могут быть как устойчивыми, так и не устойчивыми, но в любом случае систему нельзя назвать устойчивой.
3. Одна и та же система может быть как устойчивой, так и не устойчивой при разных коэффициентах усиления линейной части системы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.