Классификация автоматических систем. Методы анализа линейных систем радиоавтоматики. Характеристики линейных систем радиоавтоматики, связь между ними, страница 6

Пример:

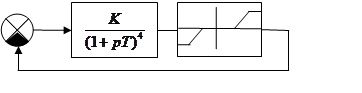
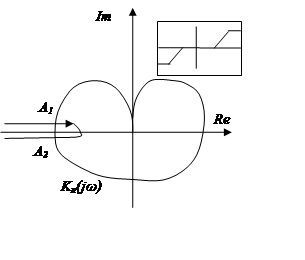
При A=A₂ возможны автоколебания. При A=A₁ автоколебаний не будет, хотя теоретически возможны.

Вопрос 23

Связь между диаграммой Гольдфарба и фазовым портретом системы. Примеры

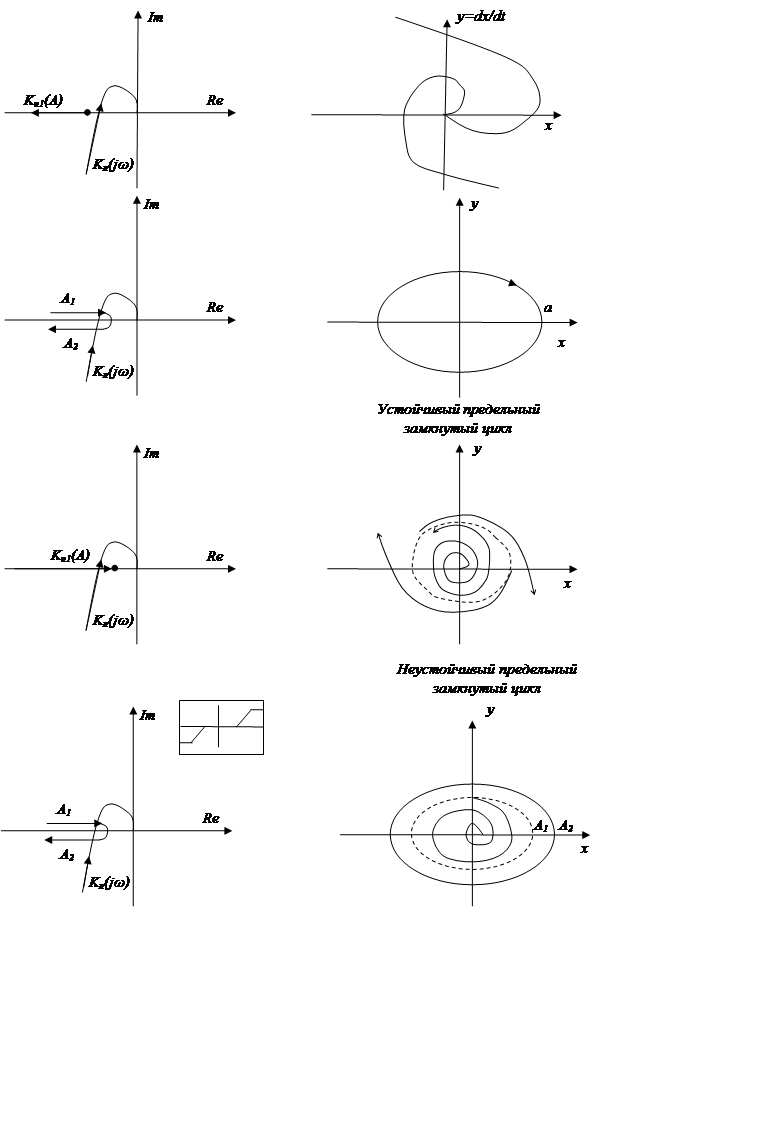
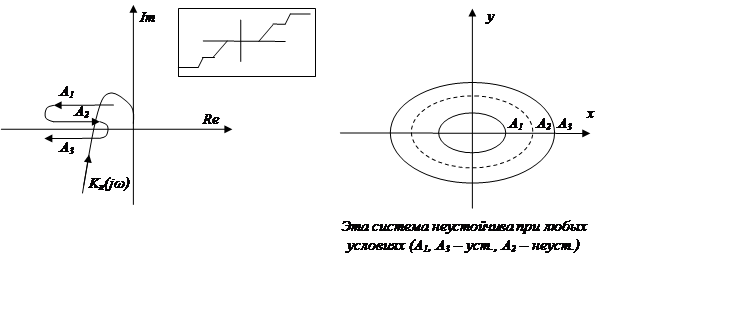
Выводы:

1.  Если годографы линейного и нелинейного звеньев на диаграмме Гольдфарба не пересекаются, но система абсолютно устойчива и на фазовом портрете будет быстрая сходимость к нулю.

2.  Если они пересекаются, то важно как они пересекаются: если годограф нелинейной части покидает пределы, очерченные годографом линейной части, то точка их пересечения соответствует предельному замкнутому устойчивому циклу, он изображается сплошной кривой, к которой стремятся все вокруглежащие фазовые траектории; если годограф нелинейной части входит внутрь линейного, то замкнутый цикл будет неустойчивым, изображается пунктирной линией, от него отталкиваются все вокруглежащие фазовые траектории.

3.  Сколько точек пересечения на диаграмме Гольдфарба, столько будет предельных замкнутых циклов (устойчивых  и неустойчивых).

Вопрос 24

Основные характеристики случайных процессов

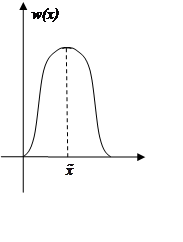
Математическое ожидание – точка наиболее вероятного нахождения функции (среднее значение):

.

.

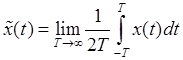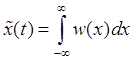Дисперсия:

.

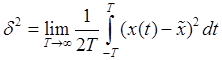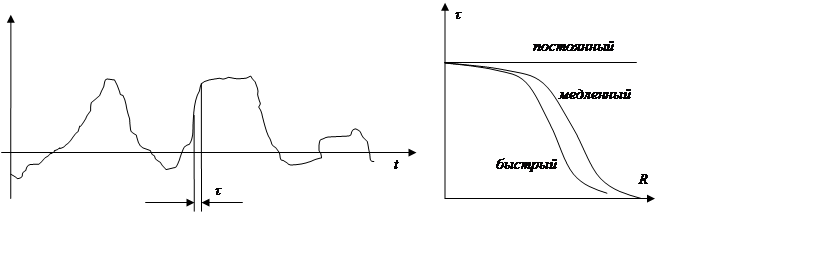
Допустим, даны два процесса: у них все три характеристики одинаковы, но скорость разная, она характеризуется двумя характеристиками – корреляционной функцией и спектральной плотностью.

Корреляционная функция отражает статическую взаимосвязь между двумя сечениями.

.

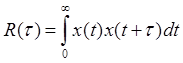Спектральная плотность – закон, по которому энергия СП распределена по частотному закону:

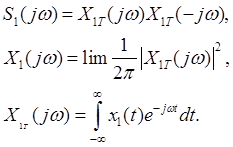
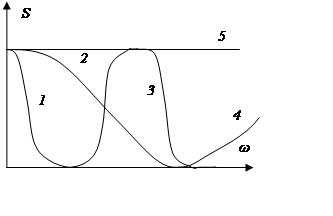
1 – СП низкочастотный

2 – в 2 раза быстрее

3 – квазиполосовой СП

4 – высокочастотный быстрый СП

5 – белый шум

Закон Фурье – чем уже график корреляционной функции, тем шире задан график СП.

Свойства КФ:

1.  КФ нулевого аргумента равна среднеквадратическому значению СП;

2.  КФ бесконечного аргумента равна квадрату среднего значения.

Вопрос 25

Теорема Винера - Хинчина

Корреляционная функция и спектральная плотность СП являются парой преобразований Фурье.

(закон Фурье: чем уже график корреляционной функции, тем шире график спектральной плотности).

Корреляционная функция отражает статическую связь между двумя характеристиками:

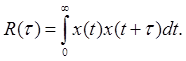
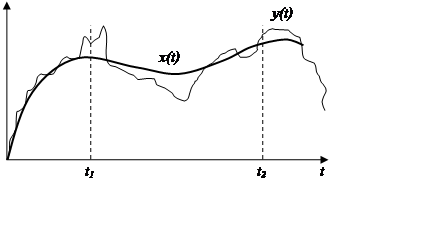
x(t₁) - x(t₂) – связь сильна, т.к. процесс медленный.

y(t₁) - y(t₂) – связь мала, т.к. процесс быстрый.

Спектральная плотность – закон, по которому энергия случайного процесса распределена по частотному диапазону.

.

Вопрос 26

Случайные процессы в линейных системах радиоавтоматики

Классификация:

1. Стационарные и нестационарные СП

Все статистические характеристики ССП со временем не меняются, в нестационарном случае – меняются.

2. Эргодические и неэргодические СП

Эргодические СП – такие процессы, когда один источник данного СП является полномочным представителем данного типа СП: усреднение по множеству даёт тот же результат, что и усреднение по времени.

Вопрос 27

Ошибки регулирования в системах радиоавтоматики при случайном управляющем воздействии

Поиск такой ошибки заменяется поиском спектральной плотности в той точке системы, сигнал в которой называется ошибкой регулирования.

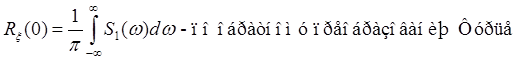
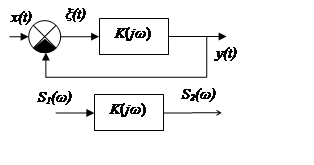
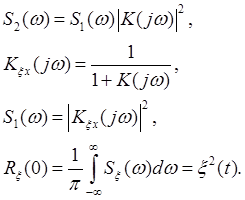
Вопрос 28

Ошибки регулирования в системах радиоавтоматики при одновременном воздействии случайного управляющего сигнала и помехи

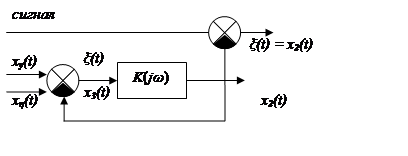
Сумматор выделяет ошибку

.

Надо, чтобы сигнал x₂(t) был равен x_у(t), т.е.

, ξ = 0, т.е. в точке x₃ полностью выделяется помеха.

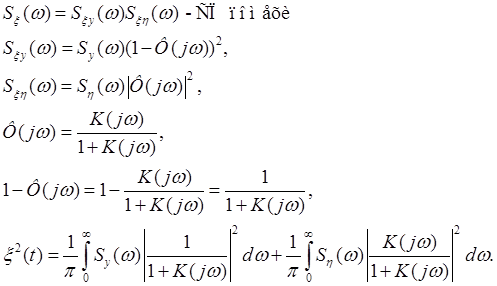
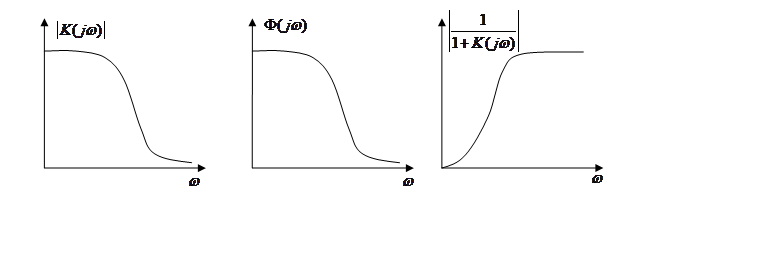
В формуле  частотные характеристики в двух интегралах обладают такой зависимостью, что там где одна мала, другая велика, где одна растёт, другая убывает. Благодаря этому мы можем уменьшить ошибку регулирования.

Для этого надо, чтобы спектральная плотность помех и воздействия находились не в одном месте, а хотя бы частично были разнесены в разные стороны, и чтобы частотная характеристика была максимально похожа на СП управляющего сигнала.