1. Связь между передаточной функцией и комплексным коэффициентом передачи:
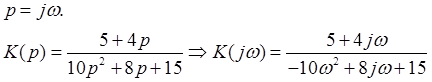
2. Связь между временными и частотными характеристиками K(jω) и g(t) – прямое и обратное преобразование Фурье:
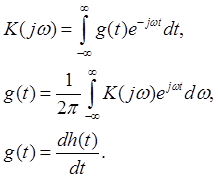
Дифференциальное уравнение:
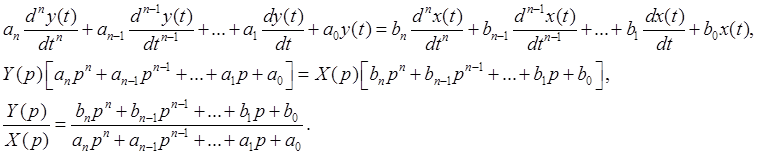
Передаточная функция системы есть отношение полиномов (коэффициенты в числителе - из правой части ДУ, в знаменателе – из левой части ДУ).
![]()
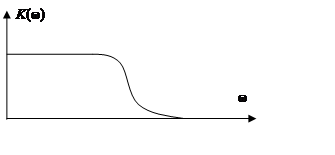
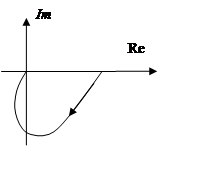
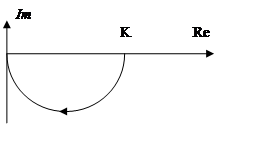
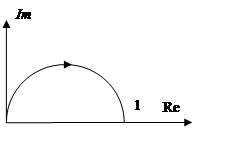
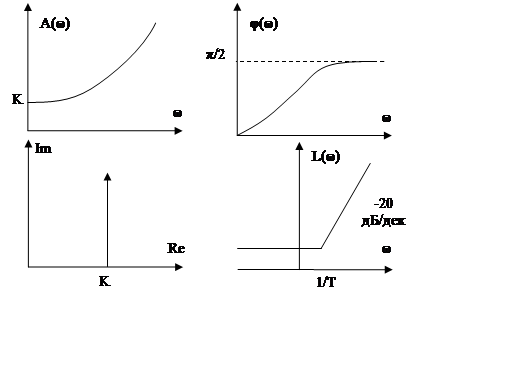
АЧХ=геом сумма от K(jw) ФЧХ=arctg(Im/Re) Годограф-Кривая, нарисованная концом вектора компл коэф-та передачи при изменении частоты от 0 до 00
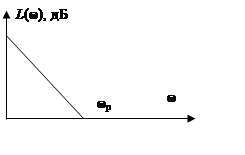
Логарифмическая АЧХ
Вопрос 4
Структурные схемы, отличие от функциональных. Примеры
Структурные схемы – набор прямоугольников, соединённых стрелками, показывающих направление распространения информации. В прямоугольниках указываются соответствующие передаточные функции.
Структурные звенья 1го порядка:
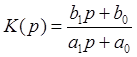 .
.
1. Безынерционное (пропорциональное) звено
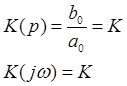

2. Инерционное
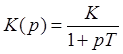
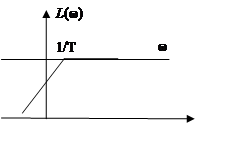
K – коэффициент усиления на постоянном токе, T – постоянная времени инерционного звена.
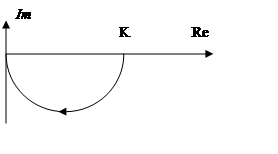
3. Идеальное интегрирующее
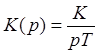
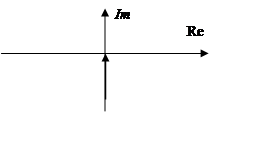
4. Дифференцирующее а) идеальное дифференцирующее звено
![]()
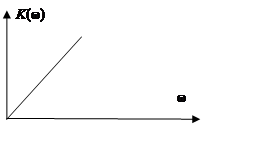
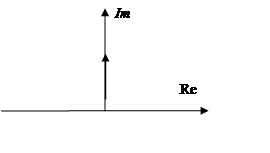
5. Реальное дифференцирующее звено
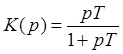
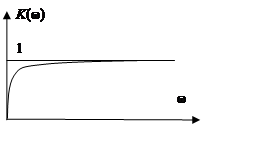
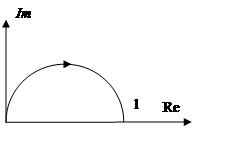
5. Упругие звенья
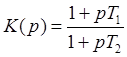
а) T1 > T2 – упругое дифференцирующее
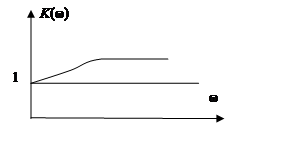
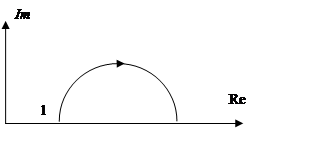
б) T1 < T2 – упругое интегрирующее
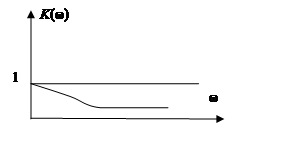
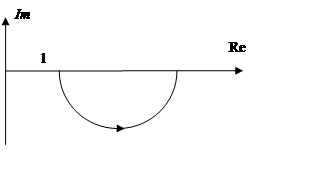
6. Форсирующее
![]()
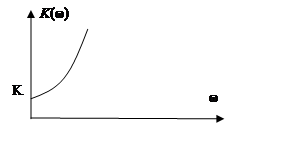
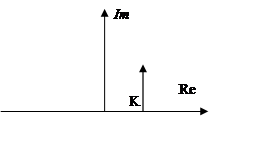
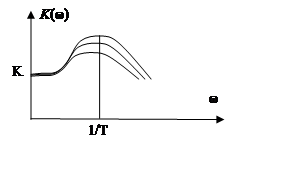
7. Колебательное
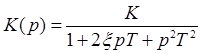
В структурных схемах используется операторный метод. В качестве описания используется передаточная функция каждого элемента. Функциональные схемы позволяют рассмотреть схему на уровне принципа работы и связей между основными элементами.
Вопрос 5
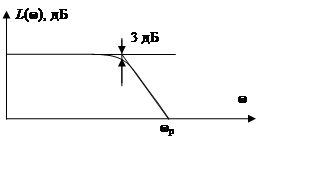
Инерционные и интегрирующие звенья, их характеристики
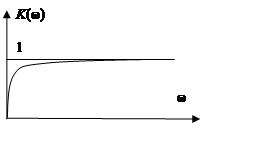
Инерционные звенья
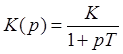 .
.
K – коэффициент усиления на постоянном токе.
T – постоянная времени инерционного звена.
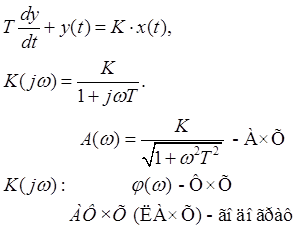
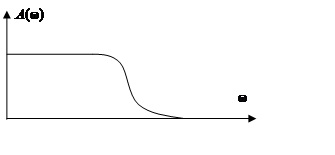
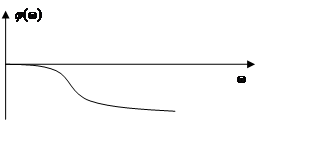
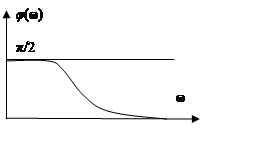
φ(ω) = 0 - arctg(ωt) = - arctg(ωt).
![]() .
.
Интегрирующие звенья:
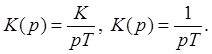
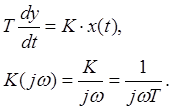
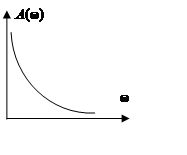
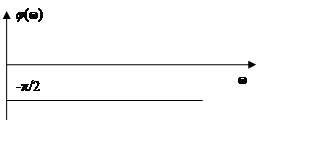
Подадим на вход ступеньку, получаем
|
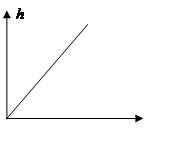
Сравним с инерционным звеном.
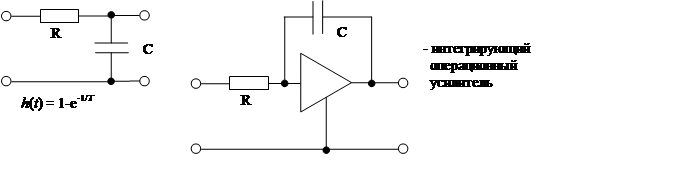
К интегрирующему операционному усилителю предъявляются требования:
K→ ∞,
Rвх → ∞,
Rвых→ ∞.
Инерционность появляется сама из-за наличия паразитных параметров.
Вопрос 6
Дифференцирующие и упругие звенья, их характеристики
1. Дифференцирующие звенья
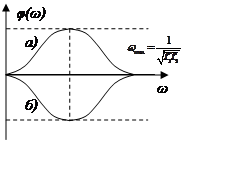
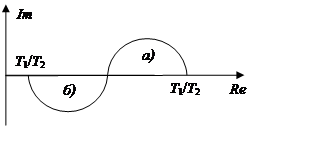
K(jω): A(ω) – АЧХ, φ(ω) – ФЧХ, АФЧХ – годограф, ЛАЧХ.
а) идеальное дифференцирующее звено
K(p) = pT, y(t)=Tdx/dt.
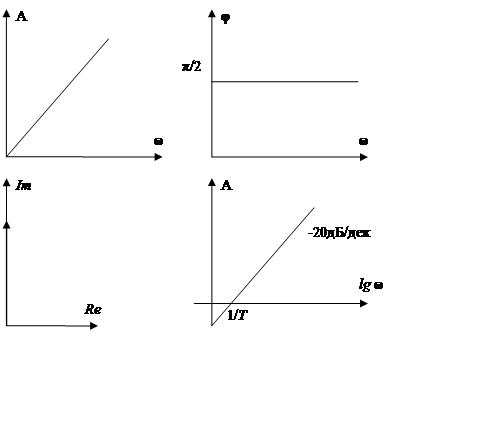
L(ω) = 20lg(ωT).
Подадим единичный импульс.
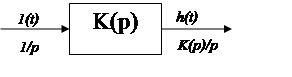
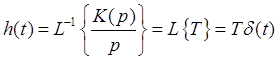 .
.
Импульсная характеристика имеет вид:
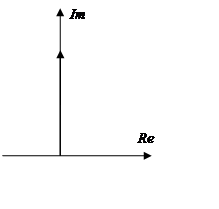
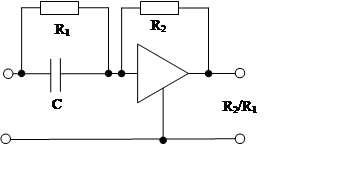
Операционный дифференциальный усилитель:
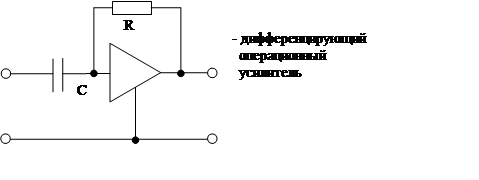
Требования к ОУ: K = -∞, Rвх → ∞, Rвых → 0
Область применения: коррекция автоматических систем.
б) реальное дифференцирующее звено
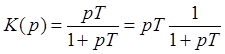 .
.
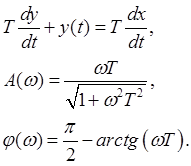
![]() .
.
Область применения: коррекция автоматических систем.
Дифференцирующие звенья поглощают астатизм и являются «противоположными» интегрирующим.
Самая простая реализация вынужденной схемы:
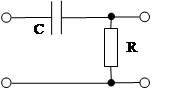
Переходная характеристика:
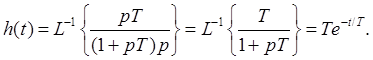
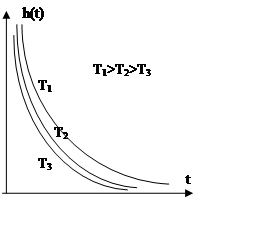
Чем больше постоянная времени, тем выше качество дифференцирования.
2. Упругие звенья
Передаточная характеристика:
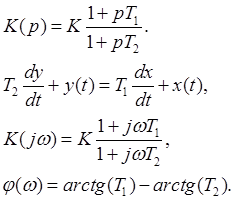
Возможны два варианта:
а) T1 > T2 (звено упругое дифференцирующее);
б) T2 > T1 (звено упругое интегрирующее).
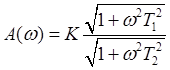
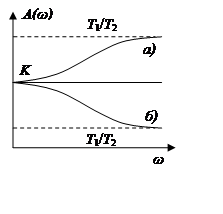
а) а) 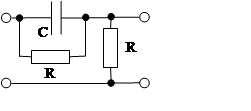 б)
б) 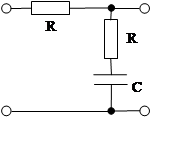
Область применения: коррекция автоматических систем с целью снятия самовозбуждения.
Переходные характеристики:
а) 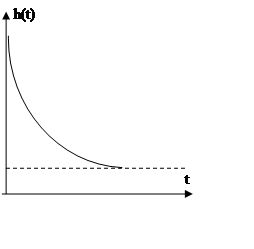 б)
б) 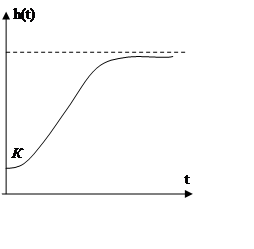
Вопрос 7
Форсирующее и колебательное звенья, их характеристики
Форсирующее звено является антиинерционным звеном.
![]() .
.
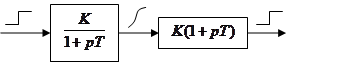
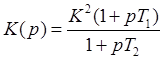 ,
,
T1 = T2: K(p) = K2.
Физически сделать трудно.
Дифференциальное уравнение:
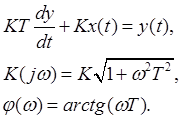
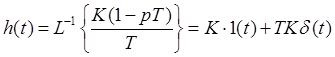 .
.
Область применения: борьба с инерционностью.
Колебательное звено:
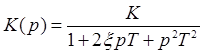 .
.
ξ – коэффициент затухания (соизмерим с 1).
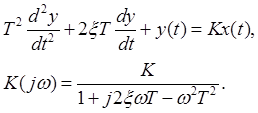
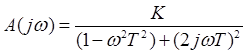 ,
, 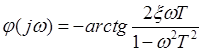 .
.
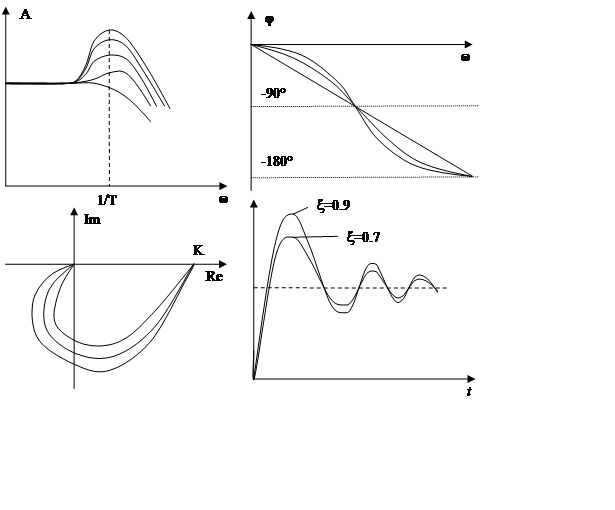
Чем меньше ξ, тем дольше происходят колебания.
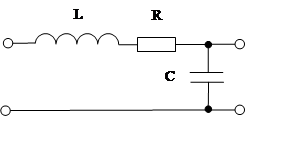
Часто встречается в автоматических системах.
Вопрос 8
Передаточные функции разомкнутых и замкнутых систем, передаточные функции ошибки от регулирующего и возмущающего воздействий
Передаточная функция (ПФ) разомкнутых систем:
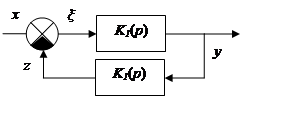
Рассмотрим следящую систему.
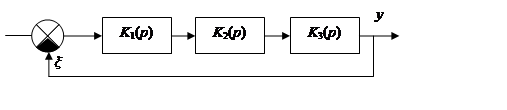
![]()
![]() - передаточная функция разомкнутой системы. Сигнал z должен
копировать сигнал x.
- передаточная функция разомкнутой системы. Сигнал z должен
копировать сигнал x.
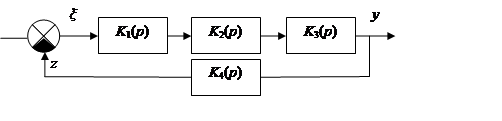
ПФ замкнутой системы
K(p) включает в себя все 3 звена.
![]() - ПФ замкнутой
системы.
- ПФ замкнутой
системы.
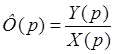 .
.
Из-за обратной связи
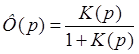 .
.
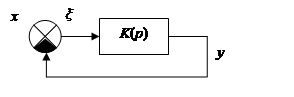
Не следящая система
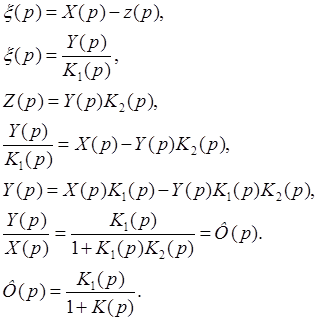
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.