Передаточная функция замкнутой системы. Характеристические полиномы разомкнутой и замкнутой системы

Министерство образования  и науки Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

_____________________________________________________________________

Кафедра Радиоприемных и Радиопередающих устройств

РАДИОАВТОМАТИКА

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №1

ВАРИАНТ № 72

Новосибирск, 2013

Задание на работу:

1. По имеющейся в исходных данных передаточной функции разомкнутой системы записать передаточную функцію замкнутой системы.

2. Записать передаточную функцию для ошибки от регулирующего воздействия.

3. Изобразить структурную схему исследуемой системы, считая систему следящей.

4.Записать характеристические полиномы разомкнутой и  замкнутой системы.

5. Исследовать систему на устойчивость по критерию Гурвица.

6. Исследовать  систему  на  устойчивость  по  критерию Михайлова методом чередующихся корней.

7. Построить годограф Михайлова с указаним масштабов по обеим осям.

8. Исследовать систему на устойчивость по критерию Найквиста.

9. Построить годограф Найквиста с указаним масштабов по обеим осям.

10. Определить запас устойчивости по модулю и по фазе.

11. Вычислить коэффициенты ошибки  и  найти  ошибку регулирования системы  в  установившемся режиме ξ(t) при заданной входной функции.

12. Построить график ξ(t) в масштабе по обеим осям.

Исходные данные:

Передаточная функция разомкнутой системы:

, где     

A= 10, B= -2(), C=0.5 (),D= 0.2

1.  Передаточная функция замкнутой системы:

Ф(р) =

Однако, с другой стороны, К(р) =  и Ф(р) =

Таким образом, Ф(р) =

2.  Запишем передаточную функцию для ошибки от регулирующего воздействия:  

3.  Изобразим структурную схему исследуемой системы:

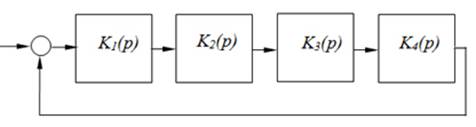
Рис.1. Структурная схема следящей системы

Исходная схема состоит из одного интегрирующего и трех инерционных звеньев.

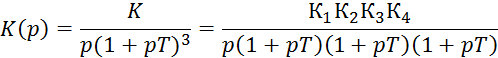
Где К=

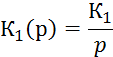
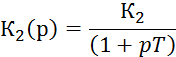
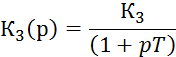
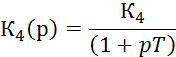
4.  Запишем характеристические полиномы для разомкнутой А(р) и замкнутой G(p) системы:

A(p) = =

=

G(p)=

= =

=

5.  Проверка системы на устойчивость по критерию Гурвица.

Проверим для начала выполнения необходимого условия устойчивости системы по критерию Гурвица, т.е положительность всех коэффициентов уравнения G(p):

Необходимое условие выполняется, значит, есть смысл проверять достаточное условие:

Получим для заданной системы следующую матрицу:

=

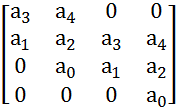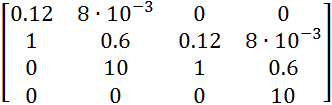
Далее необходимо вычислить диагональные определители, если все они будут больше нуля, то сможем сделать вывод об устойчивости системы.

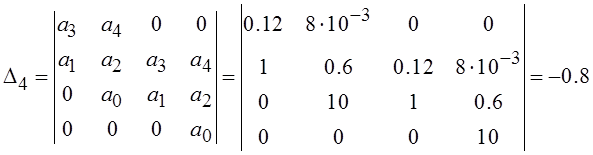
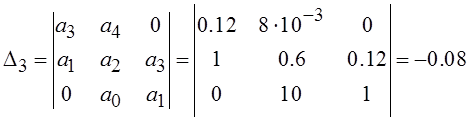
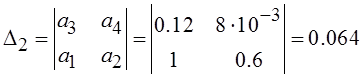
∆₃ < 0, ∆₄ < 0 – система неустойчивая по критерию Гурвица.

6.  Проведем анализ устойчивости системы по критерию Михайлова.

Преобразуем полином характеристический полином замкнутой системы, перейдя в частотную область.

G(p) =

G(j)==

=

Запишем отдельно действительную и мнимую части полученного выражения:

Re(G(j))=

Im(G(j))=

Найдем частоты пересечения мнимой оси, для чего приравняем к нулю вещественную часть и найдем корни полученного уравнения.

Re(G(j))=

Заменим переменную:

Решаем полученное квадратное уравнение.

Возвращаемся к замене. Взяв только положительные значения частот, получаем:

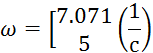
Находим частоты пересечения вещественной оси:

Im(G(j))==0

Откуда, беря только положительные частоты, получаем:

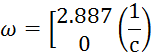
Расположим все четыре частоты пересечения осей по порядку их возрастания:    0; 2.887; 5; 7.071                                             

Как видим, рядом расположены два корня одного уравнения Re(G(j))=0 и Im(G(j))=0. Система неустойчива.

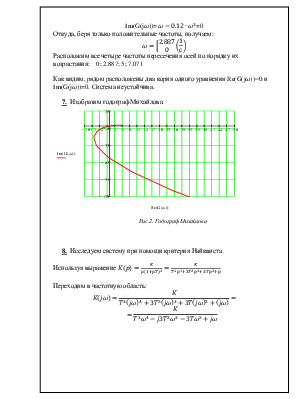
7.  Изобразим годограф Михайлова.

Рис.2. Годограф Михайлова

8.  Исследуем систему при помощи критерия Найквиста.

Используя выражение

Переходим в частотную область:

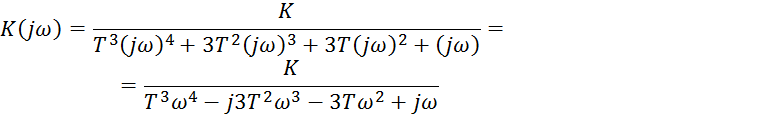
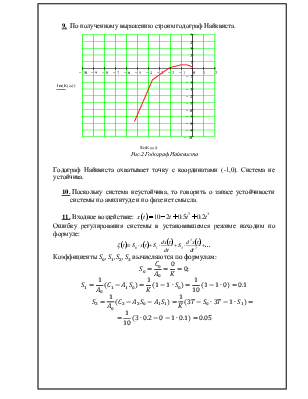
9.  По полученному выражению строим годограф Найквиста.

Рис.2 Годограф Найквиста

Годограф Найквиста охватывает точку с координатами (-1,0). Система не устойчива.

10. Поскольку система неустойчива, то говорить о запасе устойчивости системы по амплитуде и по фазе нет смысла.

11. Входное воздействие:

Ошибку регулирования системы в установившемся режиме находим по формуле:

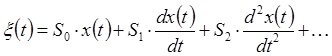
Коэффициенты

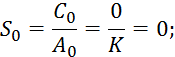
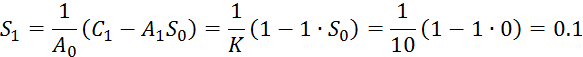
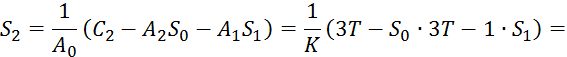
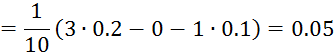
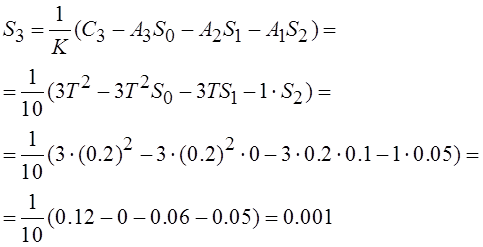
Теперь определим ошибку регулирования:

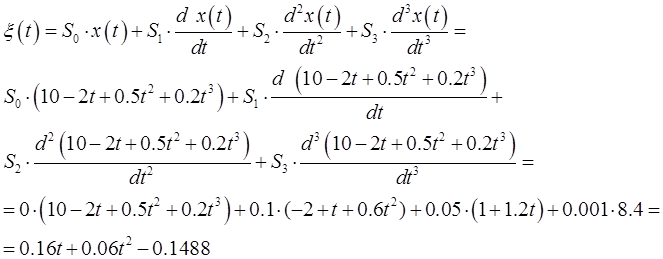
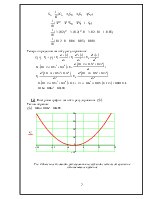
12.  Построим график ошибки регулирования .

Таким образом:

Рис. 4 Зависимость ошибки регулирования исследуемой системы от времени в установившемся режиме

Список литературы:

1. Лявданский С.Е. - «Радиоавтоматика». Методические указания к самостоятельной аудиторной работе. Новосибирск 1990 г.

2. Лявданский С.Е. - «Радиоавтоматика». Методические указания к индивидуальной работе. Новосибирск 1995 г.

3. Лявданский С.Е. - «Радиоавтоматика». Методические указания к выполнению расчетно-графического задания. Новосибирск 2010 г.