Методические указания к выполнению лабораторного практикума по дисциплине «Радиоавтоматика», страница 7

Эта запись означает, что в системе выполняется и баланс амплитуд, и баланс фаз для автоколебаний. Переписав это немного иначе, получаем:

  .

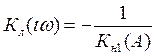Это равенство и означает, что если в системе возможны автоколебания (выполняется условие гармонического баланса), то  годографы должны пересечься. Однако, не каждому пересечению годографов на диаграмме Л.С. Гольдфарба соответствует наличие устойчивых автоколебаний. Может быть так. Что годографы пересекаются, а колебаний в системе практически не наблюдается. В этом случае говорят, что теоретически баланс фаз и амплитуд для автоколебаний вроде бы есть, но автоколебания неустойчивы, и даже если их спровоцировать внешней силой, они быстро прекратятся после снятия этой внешней силы. Так каким же пересечениям годографов линейной и нелинейной частей соответствует устойчивые автоколебания, а каким - нет? Этот вопрос в своё время детально изучил профессор Л.С. Гольдфарб и доказал следующее: автоколебания будут устойчивы в точке пересечения годографов, если при приращении аргумента А на годографе нелинейной части он выходит из пределов комплексной плоскости, очерченных годографом линейной части. Если же годограф нелинейной части входит внутрь вышеуказанной области комплексной плоскости, то автоколебания будут неустойчивыми, то есть, практически их нельзя будет наблюдать.

В таблице 3.1 приведены зависимости модуля и фазового сдвига коэффициента передачи по первой гармонике для некоторых типовых нелинейных звеньев.

В таблице 3.2 для этих же звеньев приведены годографы прямой и обратной функций комплексного коэффициента передачи нелинейных звеньев по первой гармонике.

Таблица 3.1.          

Что касается фазового портрета, то вкратце можно отметить, что строится он на так называе6мой фазовой плоскости, где по горизонтали откладывается величина исследуемой функции (обычно выход системы), а по вертикали – её первая производная. Так что ни о каком привычном для радистов фазовом сдвиге на фазовой плоскости нет даже речи. Если в системе возможны устойчивые автоколебания, то фазовая траектория, двигаясь по часовой стрелке, асимптотически приближается к замкнутой кривой (часто эллипс), называемой предельным устойчивым циклом, и будет вращаться там до выключения системы. Если же в системе невозможны автоколебания, фазовый портрет представляет собой спираль, сходящуюся в состояние покоя системы (часто начало координат).

В заключение стоит сказать, что пересечений годографов на диаграмме Гольдфарба может быть и несколько. В таком случае там будут и несколько предельных замкнутых циклов на фазовом портрете.

Список контрольных вопросов

1.Линейная часть нелинейной системы состоит из четырех  инерционных и двух форсирующих звеньев. Нелинейная часть – «зона нечувствительности». Предложите вариант диаграммы Гольдфарба системы.

2. Линейная часть нелинейной системы состоит из двух  инерционных и двух форсирующих звеньев. Нелинейная часть – «зона нечувствительности». Предложите вариант диаграммы Гольдфарба системы и фазового портрета.