Методические указания к выполнению лабораторного практикума по дисциплине «Радиоавтоматика», страница 4

Целью работы является исследование устойчивости двух различных линейных систем автоматического регулирования, а также влияние на устойчивость и запас устойчивости системы введенных в её структуру различных корректирующих звеньев. Работа выполняется в компьютерном классе на математических моделях систем. Структурные схемы двух исследуемых систем приведены ниже.

Порядок выполнения работы:

1. Открыть с рабочего стола лабораторную работу №2 по радиоавтоматике.                                                                                      Компьютер начнет вычисления и выдачу информации на монитор по программе работы. Весь объем работы состоит в следующем:

1.1. исследуется устойчивость системы №1 без коррекции (структурные схемы исследуемых систем выводятся на монитор в самом начале работы). Система №1 без коррекции содержит в своём составе три инерционных звена с одинаковыми постоянными времени ; при этом звено последовательной коррекции (упругое дифференцирующее) и звено параллельной коррекции (идеальное дифференцирующее) отключены. Коэффициент усиления системы выбран таким, чтобы без коррекции система была неустойчива. Компьютер вычислит и выведет на монитор годографы Найквиста и Михайлова, а также корни характеристического уравнения замкнутой системы без коррекции. Все эти результаты покажут неустойчивость системы без коррекции. Также на мониторе появится переходная характеристика, свойственная неустойчивым системам.

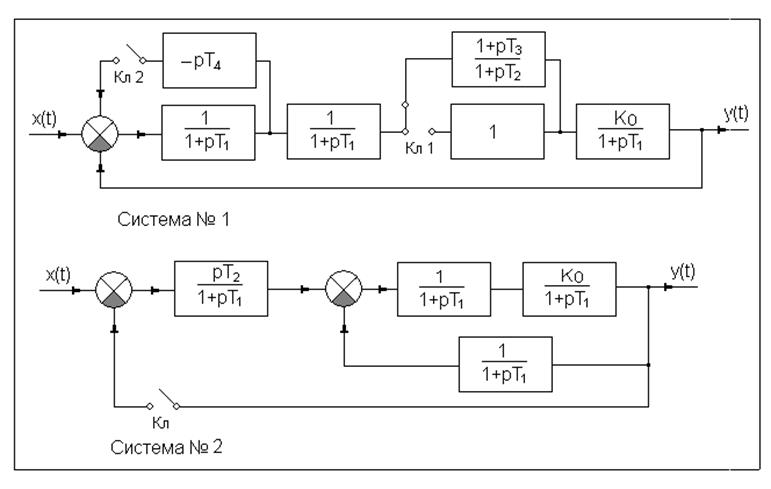
1.2. подключается упругое дифференцирующее звено последовательной коррекции  (именно такое состояние ключа Кл1 показано на схеме системы №1). Наблюдаются на мониторе оба годографа и переходная характеристика. Видно, что система стала устойчивой.

1.3. отключается звено последовательной коррекции и подключается звено параллельной коррекции. Система снова устойчива, но видно, что эффективность коррекции явно увеличилась.

1.4.  те же исследования проводятся для случая комбинированной коррекции, когда включены оба корректирующие звена. Эффективность коррекции ещё больше.

2.  исследуется система №2. Отличительной особенностью этой системы является два канала обратной связи: на главный (внешний) сумматор, и на внутренний сумматор. Эта система в данной лабораторной работе предназначена для конкретной иллюстрации того случая, когда разомкнутая система может быть неустойчивой (ключ в обратной связи разомкнут), а замкнутая система оказывается устойчивой. Как известно из критерия устойчивости Найквиста, годограф подобных систем должен охватывать точку -1 на комплексной плоскости, причем в известном направлении и конкретное число раз.

Компьютер последовательно выдаст результаты анализа устойчивости разомкнутой системы (оба годографа, переходная характеристика и корни характеристического уравнения), а затем – замкнутой системы при различных параметрах звеньев, входящих в систему №2. Полученные результаты показывают, что корни характеристического уравнения разомкнутой системы не все имеют отрицательные вещественные части, что говорит о неустойчивости разомкнутой системы. В то же время, как показывают рассчитанные годографы, замкнутая система устойчива. Можно, конечно, и замкнутую систему сделать неустойчивой, и такой пример приводится в конце работы, когда меняются некоторые параметры звеньев, входящих в систему.

Содержание отчёта.

1. Титульный лист установленного образца;

2. Результаты исследования, полученные в п,п. 1,2.

3. Аналитические выражения, по которым были рассчитаны годографы Найквиста и Михайлова. При этом рядом с каждым годографом Михайлова должен быть написан  соответствующий характеристический полином , а рядом с каждым годографом Найквиста – соответствующая передаточная функция .

3. Выводы, включающие:

- сравнительный анализ эффективности различных схем коррекции автоматических систем;

-  анализ степени совпадения полученных в процессе работы результатов с теорией;

- объяснение годографа Найквиста системы №2.

Краткие теоретические сведения