Машиностроение \ Метрология, стандартизация и сертификация

Методические указания по выполнению курсовой работы по курсу "Метрология, стандартизация, сертификация и технические измерения", страница 5

Для выбранных (или заданных) распределений f(x) и f(y) получить формулы для определения ошибок 1-го и 2-го рода (α и β).

Практическая часть. Часть 1

Открыть файл “Part1.mcd”. В пункте 1.1 задать требуемые величины:

значения Х, σх, a, b - выбрать самостоятельно, отличающиеся от заданных в примере;

значения Y и σу - не изменять.

Изучить графические зависимости на рис.1.3-1.6. Зафиксировать значения α0 и β0 при исходных значениях в таблице 1 (столбец I). Зафиксировать значения α0 и β0 в таблице 1 (столбец I) полученные в п.1.3.

Таблица 1

УСЛОВИЯ	ВЕРОЯТНОСТЬ
	I		II		III		IV		V
	Х=… σх=…		Х=… σх=…		Х=… σх=…		Y=… σу=…		Y=… σу=…
	α0	β0	α1	β1	α2	β2	α3	β3	α4	β4
1. f(x) и f(y) имеют гауссовское распределение
2. f(y) имеет нормальное распределение, f(x) – равновероятное при Х1=….. и Х2= ….
	Х1=… Х2=…		Х1=… Х2=…		Х1=… Х2=…		Х1=… Х2=…		Х1=… Х2=…
3. Для α и β, полученных в п.1.3 (для нормальных распределений обеих функций)

Примечание

При выполнении п.4.5. и последующих пунктов, привлекающих графические изображения необходимо корректировать масштаб графиков соответствующим образом для полного отображения их содержания.

Изменить Х (среднее для f(x)) в п.1.1 и оценить изменения на рис.1.3. – 1.6. Зафиксировать значения α1 и β1 в таблице 1 (столбец II).

Вернуть к исходному значению параметр Х и изменить σх. Зафиксировать значения α2 и β2 в таблице 1 (столбец III).

Вернуть к исходному значению σх и изменить Y. Зафиксировать значения α3 и β3 в таблице 1 (столбец IV). Зафиксировать значения α3 и β3 в таблице 1 (столбец IV) полученные в п.1.3.

Вернуть к исходному значению Y и изменить σу. Зафиксировать значения α4 и β4 в таблице 1 (столбец V). Вернуть σу к исходному значению. Зафиксировать значения α4 и β4 в таблице 1 (столбец V) полученные в п.1.3.

В п.1.2 задать граничные условия для равновероятного распределения функции f(x). В соответствии с рис.1.7 откорректировать значения Х1 и Х2 с целью получения наилучшей аппроксимации нормального закона равновероятным. Выполнить аналогично пункты 4.6 – 4.10, заполняя таблицу 1 для второго условия.

Сделать выводы по табл.1. Дать анализ зависимостей α и β от параметров функций f(x) и f(y).

Практическая часть. Часть 2

Открыть файл “Part2.mcd”. В пункте 2.1. задать все исходные параметры распределений f(x) и f(y). (Для удобства оценки результатов п.2.1. содержит расчет, проводимый в п.1.1.).

Объяснить зависимости α(Х) и β(Х), изображенные на рис.2.1. (Необходимо учитывать примечания, введенные в п.4.6.)

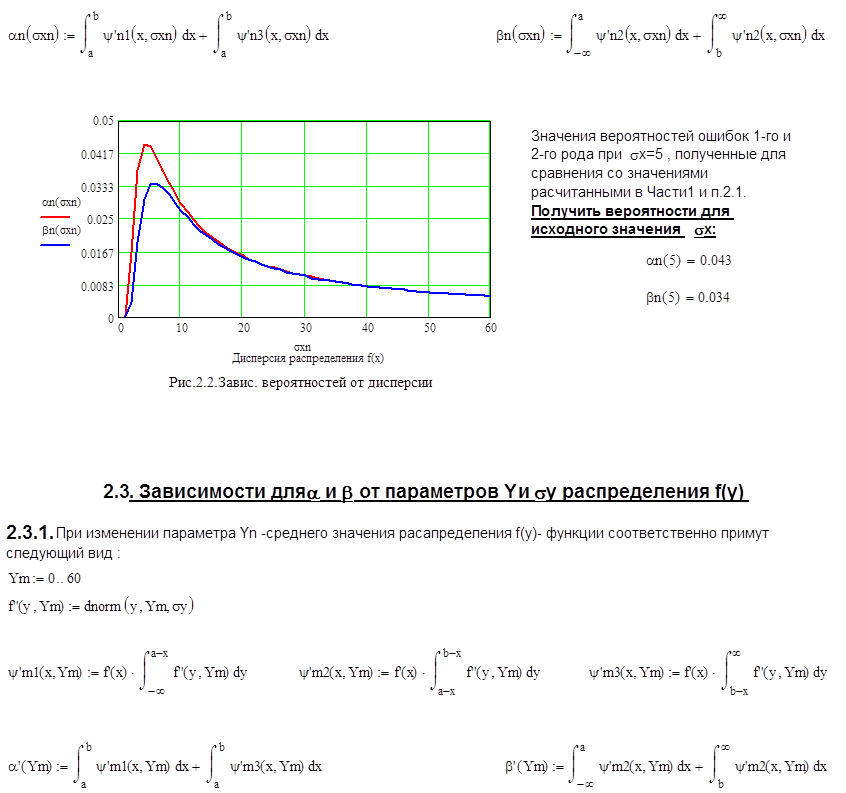
Объяснить зависимости α(σх) и β(σх), изображенные на рис.2.2.

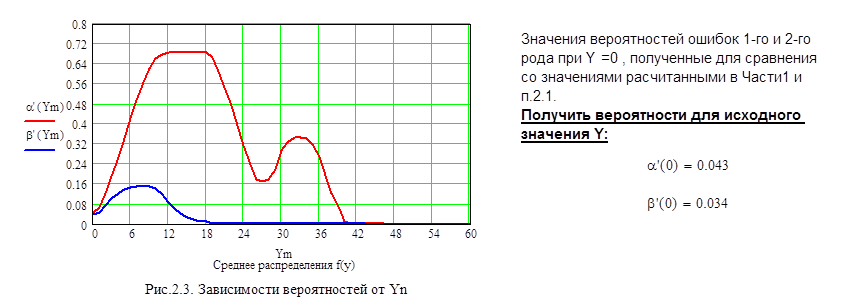
Объяснить зависимости α(Y) и β(Y), изображенные на рис.2.3.

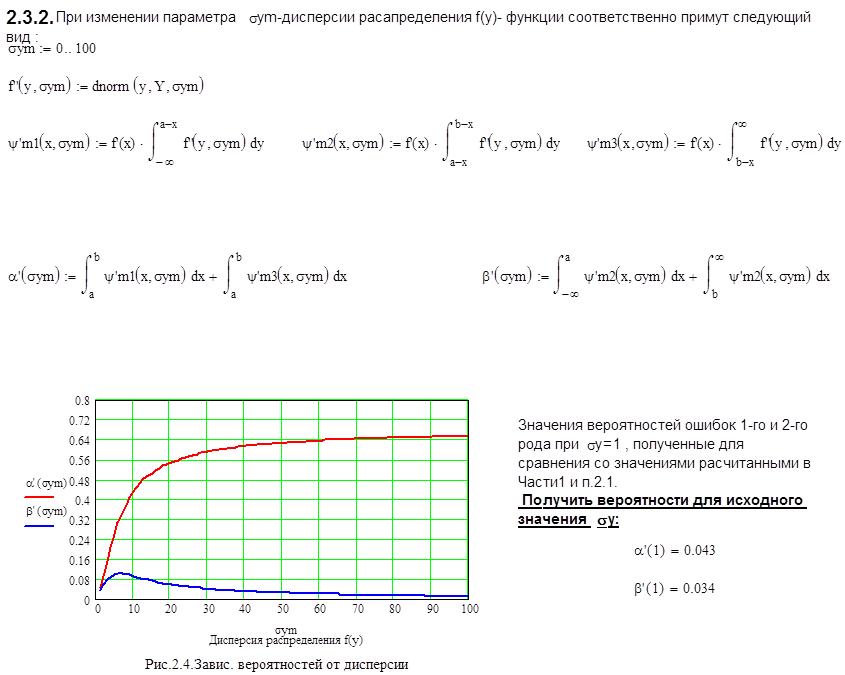
Объяснить зависимости α(σу) и β(σу), изображенные на рис.2.4.

Сделать выводы.

Оформить отчет в установленной форме.