Методические указания по выполнению курсовой работы по курсу "Метрология, стандартизация, сертификация и технические измерения", страница 3

Рассмотрим задачу контроля работоспособности с позиции общей теории проверки статистических гипотез. Пусть имеется объект контроля (ОК), состояния которого описываются значением параметра Х. Фактически, природа этого параметра может быть совершенно различной для различных ОК, следует лишь отметить, что рассматриваемый параметр характеризует качество объекта, оцениваемое при контроле. Под воздействием различного рода производственных и эксплуатационных факторов значение этого параметра от объекта к объекту и во времени случайным образом изменяется. В результате, параметр Х можно рассматривать как случайную величину с плотностью распределения f(x). Для значений параметра Х определена некоторая область (a , b) ,такая, что при выполнении условия

                                                          (1.1)

объект считается работоспособным. Условие (1.1) обычно называется условием работоспособности, а область [a , b] – допусковой областью.

В соответствии с условием (1.1) о состоянии объекта могут быть высказаны две взаимоисключающие гипотезы:  – объект работоспособен и  - объект отказал. Априорные вероятности появления событий:

;

Возможно, более точное распределение объектов этих двух категорий и является конечной целью контроля. Однако, в процессе реального контроля неизбежно появляются ошибки, и, в результате, вместо истинного значения случайной величины Х наблюдается реализация другой случайной величины:

                                                        (1.2)

где Y – случайная ошибка контроля.

Это приведет к замене решающего правила (1.1) другим:

                                                        (1.3)

Здесь  - допусковая область значений случайной величины Х, в общем случае, не совпадающая с областью [a , b].

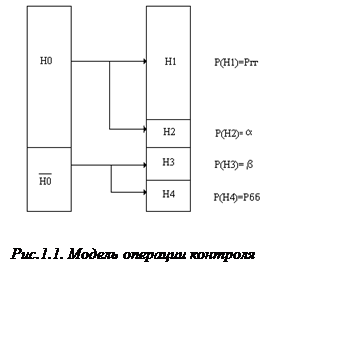
Замена (1.1) на (1.3), естественно, приводит к ошибочным решениям, в результате чего какая-то часть фактически работоспособных ОК бракуется, и, наоборот, отказавшие объекты рассматриваются как работоспособные. Таким образом, как показано на рис.1.1., при реальном контроле происходит одно из четырех несовместимых событий:

       - истинное значение параметра в пределах допуска и измеренное значение также в пределах допуска (; );

       - истинное значение параметра в пределах допуска, измеренное значение за его пределами (;  или );

       - истинное значение параметра за пределами допуска, измеренное в пределах допуска ( или ; );

       - истинное значение параметра за пределами допуска ( или ) и измеренное - за пределами ( или ).

События  и  соответствуют правильным решениям, принятым по результатам контроля, а события  и  - ошибочным. Ошибки, соответствующие событиям  и , в теории проверки статистических гипотез принято называть соответственно ошибками первого и второго рода.

Обозначим их вероятности, . Соответственно вероятности  и  - являются вероятностями правильной классификации. Условие нормировки имеет вид

2.2. Метод расчета вероятностей ошибок 1-го и 2-го рода

В результате проведения операции контроля производится разбраковка партии изделий на 3 части (доли):

первая – изделия, признанные бракованными с параметрами ниже поля допуска , т.е.;

вторая – изделия, признанные годными ;

третья – изделия, с параметрами выше поля допуска, т.е. .

Поскольку контроль параметров изделий проводится реальными измерительными приборами с конечной погрешностью измерения  , то разбиение партии изделий на три группы приведено с ошибками 1-го и 2-го рода, и  соответственно. Для определения этих ошибок вероятностей правильной разбраковки воспользуемся методом Н.А.Бородачева [2], использующего ненормированные функции распределения  для 3-х частей партии.