Методические указания по выполнению курсовой работы по курсу "Метрология, стандартизация, сертификация и технические измерения", страница 4

При этом:

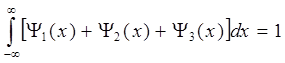.                                (1.4)

При известных моделях распределения вероятностей контролируемого параметра с плотностью f(x) и ошибок измерения с плотностью вероятности f(y) и для аддитивной модели результатов измерения

,                                                         (1.5.)

распределения  определяются по следующим формулам:

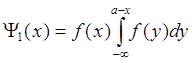;                                                (1.6)

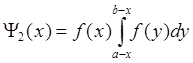;                                                (1.7)

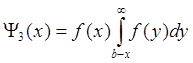.                                                (1.8)

Тогда ошибки 1-го и 2-го рода определяются следующим образом:

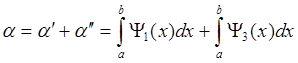;                                        (1.9)

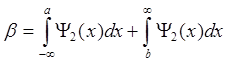.                                          (1.10)

Пусть распределение погрешности измерения является гауссовым с нулевым средним (систематическая ошибка равна нулю)

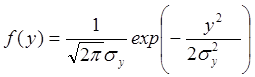.                                     (1.11)

Тогда функции распределения  примут вид:

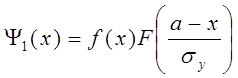;                                        (1.12)

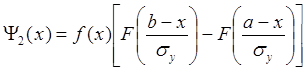;                             (1.13)

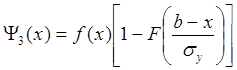,                              (1.14)

где 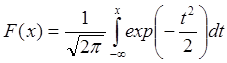 - интеграл вероятности.                                    (1.15)

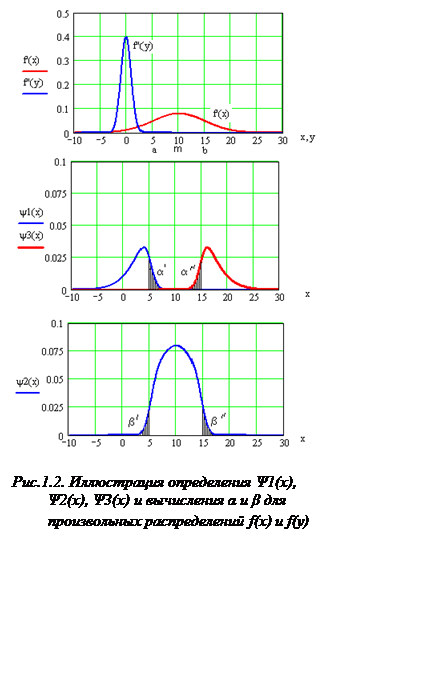
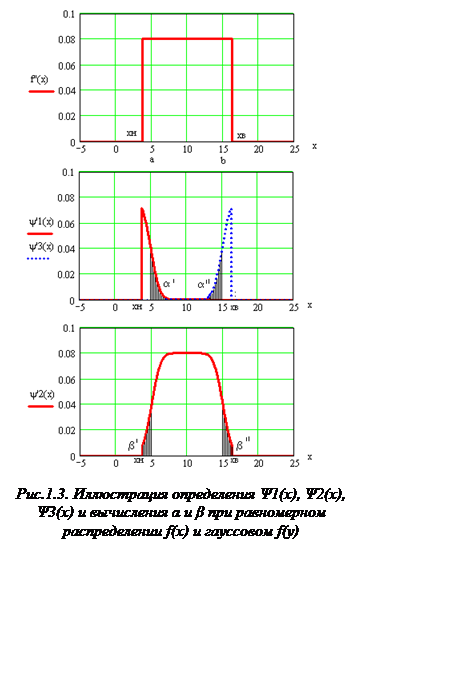
Метод получения функций  и определения с (заштрихованные площади) показаны на рис.1.2.

Для произвольного распределения  при  и нормального по Гауссу распределения ошибки  получим:

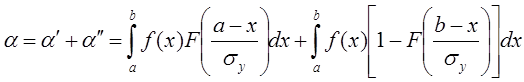;            (1.16)

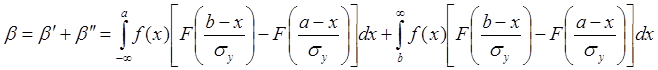. (1.17)

Интегралы (1.16) и (1.17) вычисляются численными методами.

Для этого можно воспользоваться следующими разложениями интегральной функции:

при

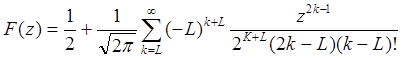                                 (1.18)

Для  можно использовать неравенства

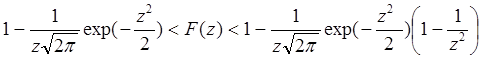                    (1.19)

Для упрощения расчетов возьмем случай равновероятного распределения :

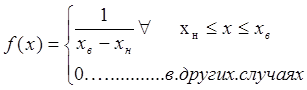                                        (1.20)

Порядок определения  и вычисление  и  показаны на рис.1.3. при гауссовом распределении ошибки .

Для этого примера  и  определяются следующими формулами:

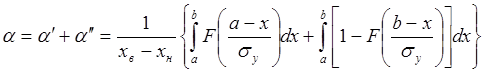;                   (1.21)

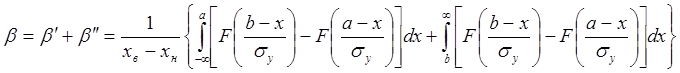;           (1.22)

Для ориентировочных расчетов применим линейную аппроксимацию:

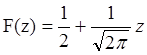,                                                 (1.23)

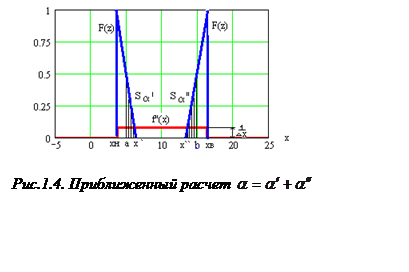
Тогда для вычисления  воспользуемся рис 1.4.

В результате получим

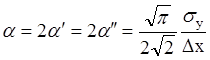                                              (1.24)

где .

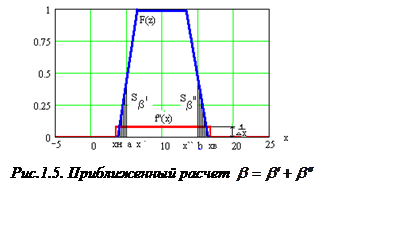
Для вычисления  воспользуемся также разложением (1.23) и рис.1.5.

Согласно рис.1.5. для нахождения  и  нужно определить заштрихованные площади  и  и умножить их на высоту  равномерного распределения.

В результате получим

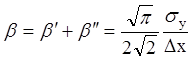.                                                (1.25)

Полученные выражения (1.24) и (1.25) позволяют очень грубо оценить ошибки при контроле и правильность выбора точности измерительного оборудования (причем, для данного расчета делали допущение о том, что среднее значение погрешности измерения равно нулю).

3. Описание работы в среде «MathCAD 2000»

Практическая часть данной работы выполняется с помощью ППП «MathCAD 2000». Для начала работы необходимо запустить два файла:

·  Part1.mcd – содержит методы определения ошибок 1-го и 2-го рода при различных функциях распределения f(x) и f(y);

·  Part2.mcd – содержит зависимости ошибок 1-го и 2-го рода от параметров распределений f(x) и f(y).

Для работы необходимо знание основных режимов работы ППП «MathCAD 2000»:

Ввод данных;

Построение графических зависимостей, корректировка графиков соответствующим образом с целью полноценного отображения их содержания.

Краткое описание дано в приложении к лаб. работе.

4. Порядок выполнения работы

Теоретическая часть

Ознакомиться с теоретическими сведениями.

Дать анализ выражений для определения ошибок 1-го и 2-го рода (риска изготовителя и заказчика).

Дать графическую интерпретацию определения  и вычисления вероятностей Ргг, Рбб, α и β при произвольных распределениях f(x) и f(y).