








Задания к лабораторной работе №1
Определение. Если результаты
наблюдений представляют собой значения случайной величины или реализации
случайного процесса в заданные моменты времени, то результат последовательности
![]() наблюдений, вектор
наблюдений, вектор ![]() с
элементами
с
элементами ![]() называется выборкой. Каждое из
значений
называется выборкой. Каждое из
значений ![]() называется выборочным. Число
называется выборочным. Число ![]() выборочных значений называют объемом
выборки. Вектор
выборочных значений называют объемом
выборки. Вектор ![]() является точкой некоторого
подмножества
является точкой некоторого
подмножества ![]() эвклидова пространства (пространства
наблюдений), подмножество
эвклидова пространства (пространства
наблюдений), подмножество ![]() называется выборочным
пространством.
называется выборочным
пространством.
Определение. Выборочное среднее
есть среднее арифметическое элементов выборки: 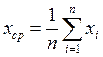 .
.
Определение. Выборочной дисперсией называютвеличину, рассчитываемую по формуле:
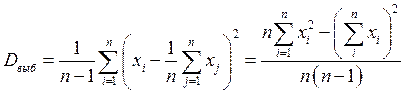 .
.
Все задания выполняются в среде Mathcad. Отчет предоставляется в виде файла.
Задание 1.
Смоделировать нормально распределенную выборку. Параметры ![]() ,
, ![]() ,
, ![]() узнать у преподавателя.
узнать у преподавателя.
|
Примечания к заданию 1: |
|
·
Функция rnorm(n,μ,σ)
возвращает вектор из · Некоторые сведения из теории вероятностей приведены в приложениях 1 и 2. Пример:
|
Задание 2.
Смоделировать равномерно распределенную на интервале ![]() выборку. Параметры
выборку. Параметры ![]() ,
,
![]() ,
, ![]() узнать
у преподавателя.
узнать
у преподавателя.
2.1.Найти дисперсию и математическое
ожидание случайной величины с распределением ![]() .
.
2.2.Найти выборочную дисперсию и выборочное среднее по элементам вектора. Сравнить с величинами, полученными в п.2.1.
|
Примечания к заданию 2: |
|
·
Функция runif(n,a,b)
возвращает вектор из Пример:
·
Функция Var(x)
возвращает выборочную дисперсию элементов вектора ·
Функция mean(x)
возвращает среднее арифметическое элементов вектора |
Задание 3.
Построить гистограммы по выборкам, полученным при выполнении заданий
1 и 2. Число столбцов для гистограммы брать равным ![]() ,
где
,
где ![]() представляет операцию округления
представляет операцию округления ![]() до большего целого.
до большего целого.
|
Примечания к заданию 3: |
|
· Гистограмма представляет собой столбцовую диаграмму, высота каждого столбца которой определяется частотой попадания выборочных значений в соответствующий интервал. Гистограмма является эмпирическим, или выборочным, аналогом таблицы или плотности распределения. Подробное описание гистограммы приведено в приложении 3. ·
Функция ceil(x)
возвращает наименьшее целое, большее либо равное ·
Оператор взятия столбца ·
Функция histogram(k,x) возвращает матрицу с двумя
столбцами. Первый столбец содержит середины Пример:
|
Задание 4.
Показать экспериментально (посредством гистограммы), что
распределение случайной величины, раной сумме двенадцати равномерно
распределенных на интервале ![]() случайных
величин, близко к нормальному
случайных
величин, близко к нормальному ![]() .
.
|
Примечания к заданию 4: |
|
· Чтобы получить выборку для построения гистограммы, надо сформировать вектор из элементов, каждый из которых представляет собой сумму двенадцати случайных чисел, взятых из равномерного распределения (см. описание функции runif(n,a,b), генерирующей нормально распределенные случайные числа, в примечаниях к заданию 2). Для выполнения этой задачи удобно воспользоваться инструментами программирования в Mathcad, краткое описание которых приведено в приложении 4. |
Определение. Отсчет сигнала — значение сигнала в определенный момент времени.
Определение. Дискретизация есть
представление сигнала в виде совокупности отсчетов, взятых через равные
промежутки времени длительностью ![]() . Величину
. Величину ![]() называют периодом дискретизации.
называют периодом дискретизации.
Задание 5.
Построить на графике отсчеты дискретизированного синусоидального
сигнала ![]() . Параметры сигнала принять
следующими: частота сигнала
. Параметры сигнала принять
следующими: частота сигнала ![]() = 20 кГц;
амплитуда
= 20 кГц;
амплитуда ![]() = 5 В; фаза
= 5 В; фаза ![]() = 0; частота дискретизации:
= 0; частота дискретизации: ![]() = 400 кГц.
= 400 кГц.
|
Примечания к заданию 4: |
|
· На рисунке ниже показаны два способа построить на графике отсчеты сигнала: формирование вектора отсчетов и определение функции с последующим заданием оси абсцисс таким образом, чтобы абсциссы точек графика совпадали с моментами взятия отсчетов.
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.