Задание 6.
Построить на графике отсчеты нескольких реализаций случайного
процесса, представляющего собой аддитивную смесь синусоидального сигнала и
нормального шума ![]() . Параметры сигнала
взять из задания 5, параметры шума принять следующими: дисперсия
. Параметры сигнала
взять из задания 5, параметры шума принять следующими: дисперсия ![]() = 1 В; среднее
= 1 В; среднее ![]() = 0 В.
= 0 В.
Задание 7.
Смоделировать сигнал ![]() на выходе
усилителя, на входе которого действует сигнал
на выходе
усилителя, на входе которого действует сигнал ![]() (см.
задание 6). Коэффициент усиления зависит от времени по закону
(см.
задание 6). Коэффициент усиления зависит от времени по закону 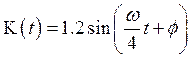 . Значения параметров
. Значения параметров ![]() и
и ![]() взять
из задания 5. Построить на графике отсчеты
взять
из задания 5. Построить на графике отсчеты ![]() .
.
Задание 8.
Рассчитать по нескольким реализациям ![]() выборочную
дисперсию сигнала на выходе усилителя в моменты времени
выборочную
дисперсию сигнала на выходе усилителя в моменты времени ![]() ,
, ![]() .
.
Определение.
Математическое ожидание случайной величины ![]() есть
число:
есть
число: 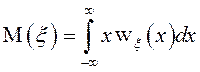 (для непрерывных распределений);
(для непрерывных распределений);
 (для дискретных распределений).
(для дискретных распределений).
Некоторые свойства математического ожидания.
1. Для произвольной
функции g
![]() , если
распределение дискретно;
, если
распределение дискретно;
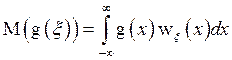 , если распределение непрерывно.
, если распределение непрерывно.
2. ![]() ,
, ![]() .
.
3. ![]() .
.
4. Математическое
ожидание суммы любых случайных величин равно сумме их математических
ожиданий:
![]() .
.
5. Математическое
ожидание произведения независимых случайных величин равно произведению их
математических ожиданий:
![]() , если
, если ![]() и
и
![]() .
Замечание: из равенства
.
Замечание: из равенства ![]() не следует
независимость случайных величин
не следует
независимость случайных величин ![]() и
и ![]() .
.
Определение.
Если ![]() , то число
, то число ![]() называется моментом порядка k
(k-м моментом) случайной величины
называется моментом порядка k
(k-м моментом) случайной величины ![]() ;
;
![]() называется абсолютным моментом
порядка k (абсолютным k-м моментом) случайной величины
называется абсолютным моментом
порядка k (абсолютным k-м моментом) случайной величины ![]() ;
;
![]() называется центральным моментом
порядка k (центральным k-м моментом) случайной величины
называется центральным моментом
порядка k (центральным k-м моментом) случайной величины ![]() ;
;
![]() называется абсолютным центральным
моментом порядка k (абсолютным центральным k-м моментом) случайной
величины.
называется абсолютным центральным
моментом порядка k (абсолютным центральным k-м моментом) случайной
величины.
Определение.
Число ![]() (центральный момент порядка 2)
называется дисперсией случайной величины
(центральный момент порядка 2)
называется дисперсией случайной величины ![]() .
.
Определение.
Число ![]() называют среднеквадратическим
отклонением случайной величины
называют среднеквадратическим
отклонением случайной величины ![]() .
.
Некоторые свойства дисперсии:
1. ![]() ;
;
2. ![]() ;
;
3. ![]() ;
;
4. ![]() , если и только если
, если и только если ![]() ;
;
5. ![]() ;
;
6. Если ![]() и
и ![]() независимы,
независимы,
![]() .
.
Совместное распределение независимых случайных величин:
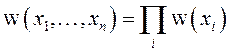
Краткая запись:
![]() .
.
Читать: случайная величина ![]() имеет
равномерное распределение с параметрами
имеет
равномерное распределение с параметрами ![]() .
.
Плотность распределения:
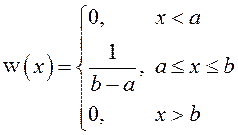 .
.
Математическое ожидание:
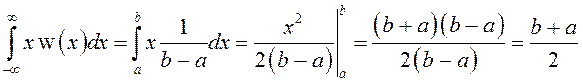 .
.
Дисперсия:
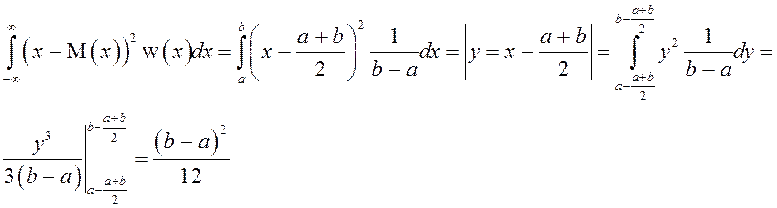
Краткая запись:
![]() .
.
Читать: случайная величина ![]() имеет
нормальное распределение с параметрами
имеет
нормальное распределение с параметрами ![]() .
.
Плотность распределения:
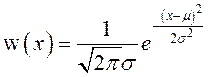 .
.
Математическое ожидание:
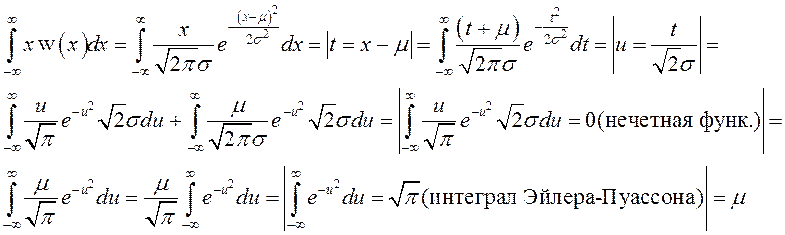
Дисперсия:
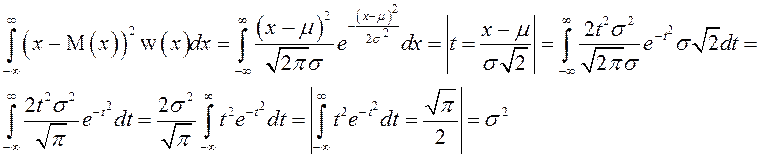
Гистограмма
строится по группированным данным. Предполагаемую область значений случайной
величины ![]() (или область выборочных данных)
делят независимо от выборки на некоторое количество интервалов (не обязательно
одинаковых). Пусть
(или область выборочных данных)
делят независимо от выборки на некоторое количество интервалов (не обязательно
одинаковых). Пусть ![]() — интервалы на прямой,
называемые интервалами группировки. Обозначим для
— интервалы на прямой,
называемые интервалами группировки. Обозначим для ![]() через
через
![]() число элементов выборки, попавших в
интервал:
число элементов выборки, попавших в
интервал:
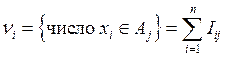 , здесь
, здесь 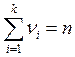 .
.
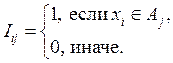
На каждом из интервалов
![]() строят прямоугольник, площадь которого
пропорциональна
строят прямоугольник, площадь которого
пропорциональна ![]() . Общая площадь всех
прямоугольников должна равняться единице. Пусть
. Общая площадь всех
прямоугольников должна равняться единице. Пусть ![]() —
длина интервала
—
длина интервала ![]() . Высота
. Высота ![]() прямоугольника над
прямоугольника над ![]() равна
равна
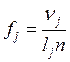 .
.
Полученная фигура называется гистограммой.
·
Вводить элементы программы можно с помощью панели Programming:
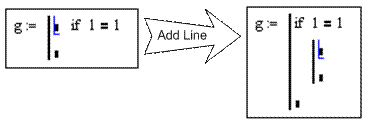
· Программа состоит из последовательно выполняемых строк. Новая строка добавляется с помощью команды Add Line.
Пример:

· Результатом выполнения программы является результат вычисления последней выполненной строки программы.
Пример:
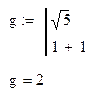
·
Оператор присваивания вводится с помощью кнопки ![]() . После
выполнения строки, содержащей этот оператор, результат выполнения выражения,
стоящего справа от знака присваивания, будет записан в переменную, стоящую
слева от знака присваивания.
. После
выполнения строки, содержащей этот оператор, результат выполнения выражения,
стоящего справа от знака присваивания, будет записан в переменную, стоящую
слева от знака присваивания.
Пример:
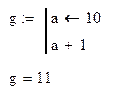
· Оператор ветвления if используется в случаях, когда некоторые действия нужно выполнять только при выполнении определенного условия. Справа от оператора if вводится условие, слева — действия, которые требуется выполнить; действия могут содержать несколько строк, их можно добавить кнопкой Add Line. Знак равенства в условии вводится комбинацией клавиш Ctrl+= . Оператор otherwise описывает альтернативную ветвь алгоритма (действия, выполняемые в случае, если условие не выполняется).
Пример:
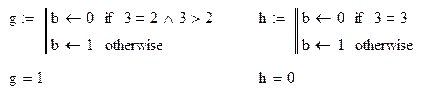
· Цикл с условием организуется с помощью оператора while. Справа от оператора вводится условия, а действия, которые следует повторять, пока выполняется условие, вводятся ниже оператора.
Пример:
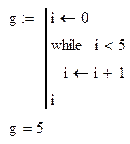
·
Цикл с параметром организуется с помощью оператора for. Действия для
повторения (называемые также телом цикла) вводятся ниже оператора. Слева от
знака ![]() вводится переменная, называемая
параметром цикла. Параметр цикла последовательно принимает значения из
диапазона, который указывается справа от знака
вводится переменная, называемая
параметром цикла. Параметр цикла последовательно принимает значения из
диапазона, который указывается справа от знака ![]() .
Тело цикла выполняется для каждого значения, принимаемого параметром.
.
Тело цикла выполняется для каждого значения, принимаемого параметром.
Пример:
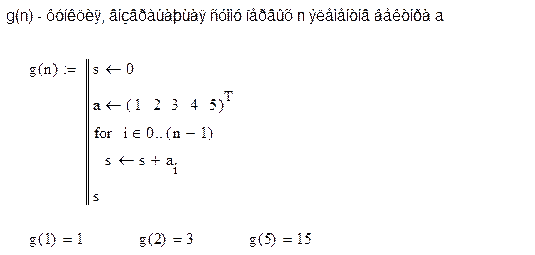
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.