Излучение радиоволн уединенными элементарными антеннами. Электромагнитное поле элементарного кардиоидного излучателя, страница 3

[формула (1.61)] = [формула (1.63)] =

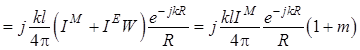,           (1.64)

где                                        .                                    (1.65)

При , т. е. когда  Ом, интенсивность электромагнитного поля в направлении сферической координаты  (т. е. по орту  декартовой системы координат) принимает удвоенное значение интенсивности поля, создаваемого в этом же направлении только магнитным или только электрическим диполем.

Выведем уравнение нормированной диаграммы направленности кардиоидного излучателя по мощности для . С учетом (1.56), (1.58) и (1.65) будем иметь:

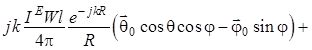
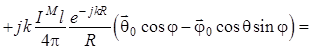
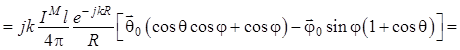
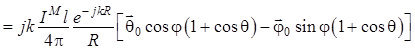,      (1.66)

где 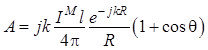     ;   ;   .   (1.67)

Затем с учетом (1.55), (1.59) и (1.65) получаем:

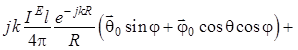
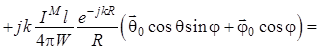
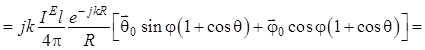
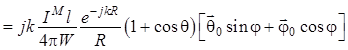,            (1.68)

здесь                            ; .                            (1.69)

Запишем значение комплексной амплитуды векторного уравнения Пойнтинга:

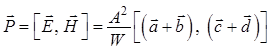.                    (1.70)

С учетом того, что

,                       (1.71)

значение комплексной амплитуды векторного уравнения Пойнтинга будет:

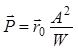.                                       (1.72)

Плотность потока мощности излучения  (подчеркнем – величина скалярная) элементарного кардиоидного излучателя есть поток мощности через небольшую площадку  на сфере очень большого радиуса, в центре которой расположен излучатель, деленный на площадь этой небольшой площадки при . Доказано [4, 6], что предел этого отношения (т. е. плотность потока мощности) численно равен модулю среднего за период высокочастотного колебания значения  вектора Пойнтинга:

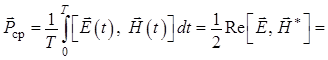
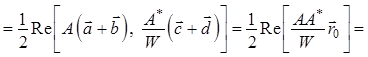
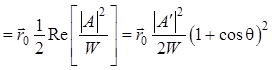,                    (1.73)

где «звездочка» (*) означает комплексную сопряженную величину; .

Из последней формулы следует, что наибольшее значение  плотности потока мощности  будет иметь место в направлении орта  (в этом направлении угол  равен нулю: ) при любых значениях угла :

.

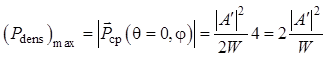Тогда нормированная пространственная характеристика направленности  (иными словами, диаграмма направленности) по мощности элементарного кардиоидного излучателя определяется как

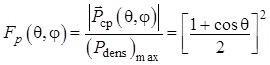.     (1.74)

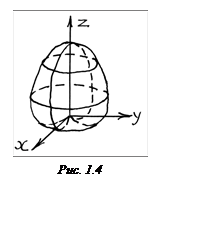
Эта характеристика, будучи независимой от угла , в любом сечении плоскостью, проходящей через ось  (орт ), представляет собой квадрат кардиоиды (рис. 1.4). Отсюда и проистекает название этого элементарного излучателя.

1.5. Электромагнитное поле элементарного турникетного излучателя

Рассмотрим излучающую систему, образованную двумя электрическими диполями Герца одинаковой длины , расположенными вдоль осей X и Y плоскости XOY так, как указано на рис. 1.5. Такая система называется элементарным турникетным излучателем и является прототипом объемных и печатных турникетных антенн. При этом фазовый сдвиг между возбуждающими осевыми токами  и  в рамках «тонкоцилиндровых» ограничений равен  (иными словами, возбуждение осуществляется во временной квадратуре; напоминание: речь идет о комплексных амплитудах):

.                                     (1.75)

Проанализируем структуру электромагнитного поля такой системы в произвольной точке дальней зоны Фраунгофера ().