Излучение радиоволн уединенными элементарными антеннами. Электромагнитное поле элементарного кардиоидного излучателя

1.4. Электромагнитное поле элементарного кардиоидного излучателя

Пусть излучающая система образована двумя диполями, лежащими в плоскости XOY (рис. 1.3), один из которых – электрический, а другой – магнитный. Пусть электрический диполь несет на себе в направлении отрицательных значений Х осевой ток с комплексной амплитудой , а магнитный диполь – в направлении отрицательных значений Y осевой ток с комплексной амплитудой  (здесь и далее для обозначения комплексной амплитуды тока проводимости используется как символ , так и символ ):

, .                            (1.30)

Полагаем длины диполей одинаковыми и равными , а возбуждение диполей – синфазным. О том, как технически осуществить синфазное возбуждение, подробно сообщается в курсе лекций по дисциплине «Устройства СВЧ и антенны». Оценим структуру электромагнитного излучения такой системы в произвольной точке дальней зоны Фраунгофера ().

Рис. 1.3

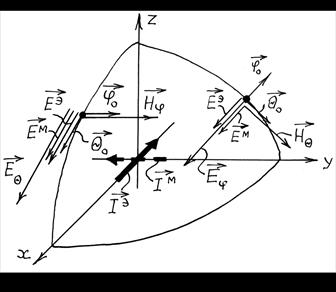
Поставленную задачу решим на основе метода суперпозиции полей, полагая, что комплексные амплитуды соответствующих векторных напряженностей  итогового поля равны сумме тех же величин, обусловленных каждым из диполей (иными словами: каждым из излучающих токов) [4, 6]:

, .                          (1.31)

Для дальнейших преобразований целесообразно использовать векторное уравнение Гельмгольца

                    (1.32)

относительно комплексной амплитуды  векторной напряженности электрического поля, обусловленного магнитным током с комплексной амплитудой , формируемой по заданной в пространстве комплексной амплитуде векторной объемной плотности  . Как известно [4], его решение формируется из произведения ротора тока на скалярную функцию Грина  свободного пространства:

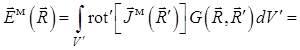
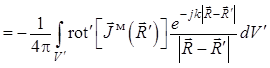,                    (1.33)

где

.

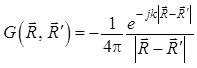Здесь «штрих» у ротора означает, что эта векторная операция (фактически: покоординатное дифференцирование проекций векторной функции) проводится по штрихованным координатам, принадлежащим диполю. Выполнение этой операции трудоемко и ненаглядно (громоздко), а потому целесообразно в соответствии с рекомендациями работы [4] получить более удобную для анализа запись уравнения (1.33). Для этого обозначим:

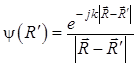,        ,                (1.34)

а также учтем известное соотношение векторного анализа:

.                       (1.35)

Тогда уравнение (1.33), фактически содержащее произведение , примет с учетом (1.35) вид

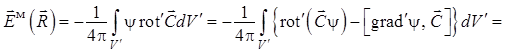
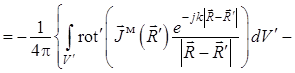
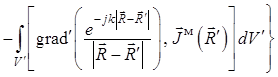.                   (1.36)

Возьмем любую замкнутую поверхность , охватывающую некий объем , в который вложен магнитный диполь (объем ) так, что поверхность  с поверхностью диполя  не соприкасается. Преобразуем первый интеграл уравнения (1.4.7) при помощи формулы, являющейся аналогом уравнения (теоремы) Остроградского–Гаусса для ротора [4]:

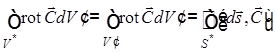,                   (1.37)

где учтено, что объемный интеграл по «разностному» объему, заключенному между поверхностью  и , равен нулю (в «разностном» объеме нет сторонних источников магнитного тока). Тогда получаем:

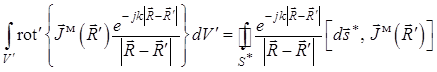.    (1.38)

Последний поверхностный интеграл, бесспорно, равен нулю, так как на замкнутой поверхности , охватывающей диполь и не соприкасающейся с ним, магнитных токов с плотностью  нет. Поэтому равен нулю левый интеграл в (1.36), а в формуле (1.38) остается только второй интеграл.

Далее нам понадобится понятие градиента длины направленного отрезка . Длина этого отрезка  есть скаляр, и можно определить градиент этого скаляра, полагая, что изменяются координаты точки наблюдения ():

,                    (1.39)

где символом обозначен орт разностного вектора . Вместе с тем можно фиксировать точку наблюдения, а изменять положение точки в излучающей системе (в данном случае – на магнитном диполе), т.е. точки интегрирования (). В этом случае длина разностного вектора  образует скалярное поле с градиентом

.                 (1.40)

Здесь «штрих» у градиента означает дифференцирование по «штрихованным» (антенным или дипольным) координатам.

Кроме того, далее понадобится формула дифференцирования сложной функции:

.                           (1.41)

Используя теперь формулы (1.40) и (1.41), можно записать:

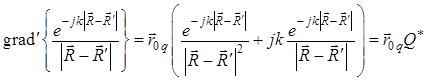.     (1.42)

В результате уравнение (1.33) для электрического поля примет вид

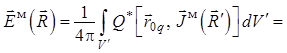
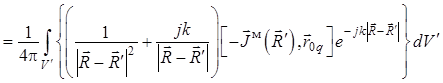.   (1.43)

Таким образом, для расчета составляющих  полного поля  кардиоидного излучателя, входящих в формулу (1.31) и обусловленных магнитным током  с объемной плотностью , должна быть использована сначала формула (1.33) , а затем второе уравнение из системы Максвелла для ситуации без источников в дальней зоне Фраунгофера :

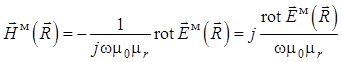.             (1.44)

Аналогично проводятся преобразования формулы для комплексной амплитуды  векторной напряженности магнитного поля, обусловленного электрическим диполем, несущим на себе электрический ток с комплексной амплитудой  и соответствующей векторной объемной плотностью . Упомянутая формула представляет собой решение векторного уравнения Гельмгольца:

                   (1.45)

и записывается в виде

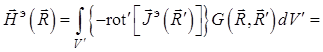
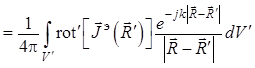.                      (1.46)

В результате приходим к уравнению для составляющей  полного поля кардиоидного излучателя:

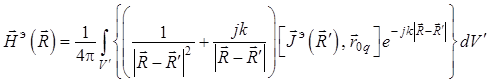, (1.47)

а используя первое уравнение из системы Максвелла для точек дальней зоны Фраунгофера без сторонних источников, получаем выражение для составляющей  полного поля кардиоидного излучателя:

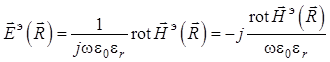.              (1.48)

Теперь можно приступить к анализу поля элементарного кардиоидного излучателя. Прежде всего в точках дальней зоны Фраунгофера можно пренебречь (отбросить) слагаемыми в уравнениях (1.43) и (1.47), содержащими множитель . Затем, поскольку плотности  токов в диполях соответственно от координат X и Y не зависят, после перехода к поверхностным интегралам по сечениям диполей  с учетом «тонкоцилиндровых» ограничений [4, 6] будут справедливы следующие уравнения:

 

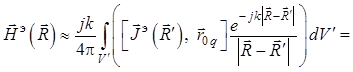
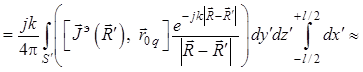
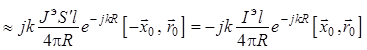;           (1.49)

 

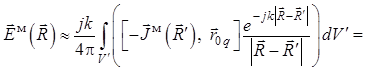
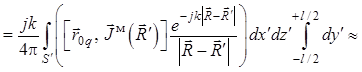
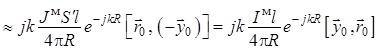,         (1.50)

где , .

В последних двух формулах учтено, что для точек дальней зоны орт  разностного вектора  практически совпадает с ортом  сферической системы координат: ; для знаменателей формул (1.49), (1.50) разностный вектор  практически равен радиусу-вектору  точки наблюдения: . Кроме того, учтено, что для экспонент в точках дальней зоны:

,                    (1.51) так как .