Излучение радиоволн уединенными элементарными антеннами. Электромагнитное поле элементарного кардиоидного излучателя, страница 2

Таким образом, составляющие  определены через сторонние токи  (формула (1.30)) и возможно дальнейшее продвижение в анализе поля кардиоидного излучателя. Это продвижение будет опираться на формулы, связывающие орты декартовой и сферической систем координат [7]:

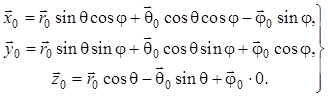               (1.52)

С учетом первого уравнения этой системы имеем:

,                          (1.53)

а с учетом второго уравнения получаем:

 

.                            (1.54)

Тогда из формул (1.49) и (1.50) формируется окончательная запись уравнений для составляющих :

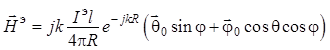,              (1.55)

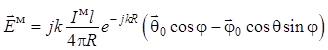.              (1.56)

Далее для нахождения составляющей  используем уравнение (1.48) в сферических координатах:

 

 

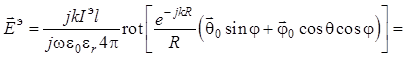
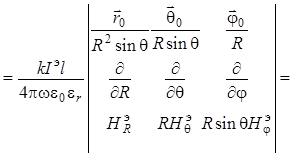
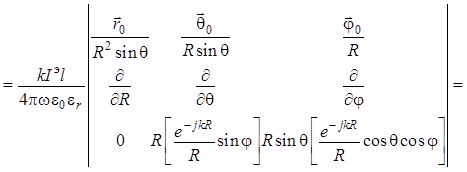
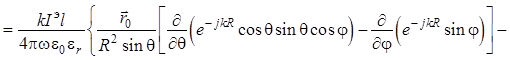
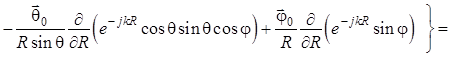
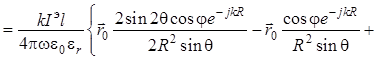
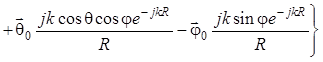.               (1.57)

В последнем выражении для точек дальней зоны Фраунгофера можно пренебречь слагаемыми, содержащими множитель . Тогда с учетом (1.13) получаем:

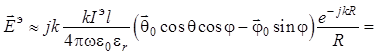
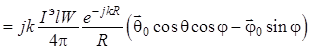.                (1.58)

Теперь для нахождения последней составляющей  поля кардиоидного излучателя применяем уравнение (1.44) в сферических координатах:

.

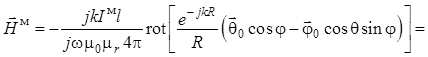
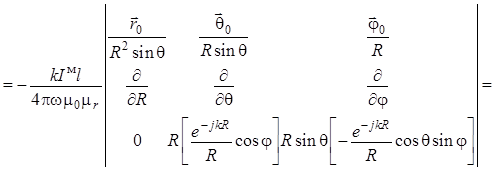
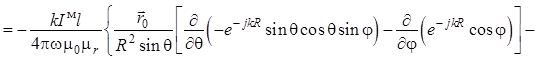
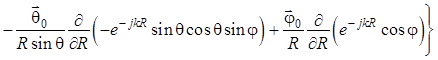Пренебрегая составляющими, содержащими множитель , получаем:

 

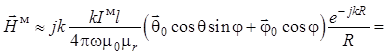
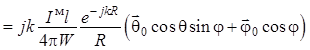.                (1.59)

Прокомментируем свойства электромагнитного поля кардиоидного излучателя, взяв за основу вектор , так как этот вектор характеризует поляризационные свойства радиоизлучения. Вначале выберем полуплоскость XOZ для  (рис. 1.3), где выполняются условия:

.                        (1.60)

Используя уравнения (1.31), (1.56) и (1.58), можно записать:

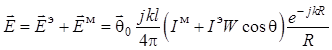.              (1.61)

Если , что означает синфазное возбуждение диполей с соответствующими амплитудами  токов, то согласно (1.61) наиболее интенсивным излучение будет в направлении положительных значений Z (). В направлении отрицательных значений Z () излучение отсутствует. Вектор  лежит в плоскости XOZ, что означает строго линейную поляризацию излучения кардиоидной системы (рис. 1.3).

Выберем теперь полуплоскость YOZ для , где выполняются условия:

.                      (1.62)

Используя уравнения (49), (74) и (76), получаем:

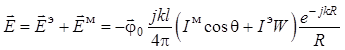.             (1.63)

Теперь при синфазном возбуждении диполей () наиболее интенсивное излучение будет опять в направлении положительных значений Z (), а в направлении  излучение отсутствует. Вектор  имеет составляющую только по углу  (рис. 1.3), т. е. излучение имеет строго линейную поляризацию.

Аналогично можно проанализировать свойства поля и в других частях пространства. Результаты анализа свидетельствуют о том, что кардиоидный излучатель формирует строго линейно поляризованное радиоизлучение. При этом плоскость поляризации всегда проходит через две прямые (два орта). Первый орт есть орт направления излучения, в данном случае – это орт  сферической системы координат. Второй орт есть орт прямой (оси), вдоль которой расположен электрический диполь Герца, в данном случае  это орт  декартовой системы координат.

Если более детально проанализировать уравнение (1.63) для  в полуплоскости для , а также смотреть при этом на рис. 1.3, то будет ясно, что при неограниченном приближении текущей точки наблюдения к положительной полуоси  (т. е. при неограниченном уменьшении угла : ) ее орт  становится противоположно направленным орту  для точки наблюдения, лежащей в плоскости  для . Отсюда следует полная эквивалентность (1.61) и (1.63) при неограниченном уменьшении угла :