Расчёт планетарной передачи. Расчёт конической передачи, страница 3

По нагрузке  рассчитывают подшипники сателлитов. При расчёте валов предполагается неизбежная неравномерность распределения нагрузки между сателлитами, связанная с неточностью изготовления колёс и различными фазами зацепления (однопарное или двухпарное), неточностью изготовления других деталей и монтажа. При наличии «плавающего» солнечного или корончатого колеса считается, что два зацепления передают 40% полной нагрузки F_n, а третье — 20%. В результате образуется неуравновешенная нагрузка (рис. 12).

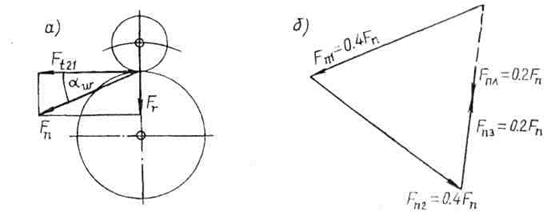
Рис. 12. Силы в зацеплениях планетарной передачи

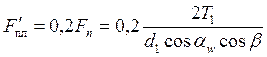.                               (64)

Неуравновешенная сила, действующая на вал водила со стороны его осей, приблизительно в два раза больше силы; её прикладывают посередине сателлитов:

.

При расчёте валов I и III (рис. 10) на прочность силы  и  прикладывают в направлении, увеличивающем напряжения и деформации, т.е. в направлении наибольшей консольной нагрузки от соседних передач (см. разд. 19).

12.5. Частоты вращения колёс

При расчёте числа циклов нагружения и подборе подшипников следует знать относительные частоты вращения колёс. Число циклов нагружения солнечного колеса определяют по формуле (20), в которой принимают

.                                                         (65)

Частота вращения наружного кольца подшипника относительно оси водила:

.                                 (66)

Частота вращения водила .

Исходя из того, что толщина обода сателлита должна быть не менее 2,25т, максимально допустимый диаметр наружного кольца подшипника

.                                                    (67)

          Пример 8. Рассчитать планетарную передачу с прямыми зубьями по схеме рис. 10 по следующим исходным данным: мощность P₁ = 5 кВт; частота вращения п₁ = 950 об/мин; передаточное отношение   = 7; число сателлитов п_с = 3; ресурс t_S = 16000 ч.

Решение.

1)  Подбор чисел зубьев и проверки – формулы (48)…(51). Принимаем z₁= 18, тогда z₃= 18·(7 – 1) = 108. Проверяем условие сборки: (z₁ + z₃)/n_c = (18 + 108)/3 = 42 (целое число).

Число зубьев сателлитов z₂ = (z₃ – z₁)/2 = (108 – 18)/2 = 45. Условие соседства (z₁ + z₂)·sin(p/n_c) – z₂= (18 + 45)×sin120° – 45 = 54,6 – 45 = 9,6 > 2.

При z₂ = 45 интерференции нет (табл. 13). Проверяем передаточное отношение:  = 1 +108/18 = 7.  Все проверки выполнены.

2)  Материалы и допускаемые напряжения. Принимаем для колёс сталь 45 (термообработка — улучшение) с твёрдостью Н = 269…302НВ (табл. 6). Допускаемое контактное напряжение [11]:

.

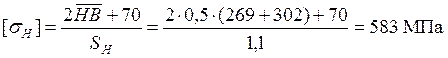Допускаемые изгибные напряжения [11]:

.

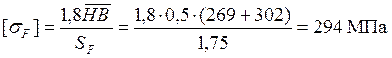3)  Кинематические расчёты.Крутящий момент на валу солнечного колеса T₁ = 9550P₁/n₁ = 9550 × 5/950 = 50,26 Н×м. Определяем КПД редуктора. Принимаем h= 0,96 (Прил. А). КПД обращённого механизма  = h²= 0,96² = 0,92. КПД планетарной передачи – формула (56):

.

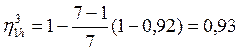Крутящий момент на водиле – формула (55):

Т_h = 50,26 × 7 × 0,93 = 327,2 Н×м.

Момент на корончатом колесе:

= 50,26 × (108/18) × 0,96² =  277,9 Н×м.

Проверка:

Т_h– Т₃ – Т₁ = 327,2 – 277,9 – 50,26 @ 0.

Частота вращения водила:

= 950/7 = 135,7 об/мин.

Относительная частота вращения солнечного колеса:

= 950 – 135,7 = 814,3 об/мин.

Относительная частота вращения наружного кольца подшипника сателлита:

= (950 – 135,7) × 18/45 = 325,7  об/мин.

Принимаем коэффициент ширины y_а= 0,25; передаточное число и = z₂/z₁ = 45/18 = 2,5 (шестерня — солнечное колесо). Принимаем длительную работу и коэффициенты К_Hд = К_Fд = 1. Принимаем ориентировочно коэффициент нагрузки К_H = К_F = 1,2. Расчётный момент:

Н×м.

4)  Межосевое расстояние из расчёта внешнего зацепления на контактную выносливость:

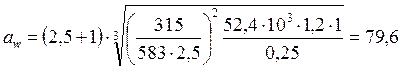 мм.

Модуль зацепления:

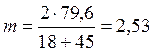 мм. 

5)  Геометрические параметры. Принимаем m = 2,5 мм. Делительное межосевое расстояние:

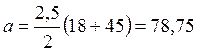 мм.

Принимаем a_w = 80 мм по ГОСТ 6636 (Прил. В). Коэффициент воспринимаемого смещения:

Угол зацепления: