Проектирование принципиальной схемы процессора для вычисления функции log2(x) методом “цифра за цифрой”, страница 3

На каждом из этапов итерационная последовательность строится путем вычисления k – ых частных сумм  ряда одного из типов констант.

Для выполнения двух указанных этапов необходимо выполнение только двух типов операций алгебраического сложения и сдвиг.

Приведем пример вычисления первого и второго этапа функции  для двоичной системы счисления. Начальным значением итерационной последовательности первого этапа является аргумент функции, предел последовательности единица. При этом выбирается значение  таким образом, чтобы получить

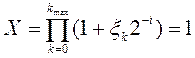
с заданной степенью точности. С этой целью используют соотношение , где  – разность между k – ым частным произведением 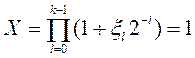 и единицей.

На втором этапе, взяв начальное значение последовательности равным 0, вычисляю произведение действительных чисел, используя найденный набор  

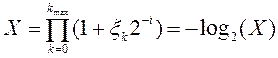
Пределом последовательности является значение функции со знаком минус.

Следует отметить, что иногда алгоритмы не дают правильный результат, когда входные значения выходят за так называемую область сходимости.

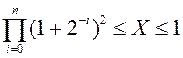 или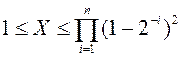 

Для того чтобы привести аргументы у области сходимости можно воспользоваться масштабированием.

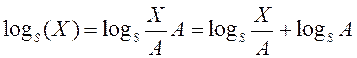
Для нашего примера не требуется масштабирования.

Рекуррентные отношения для вычисления :

,

,

,

,

,

,

,

,

,

.

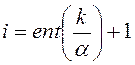4.                      Алгоритм вычисления , где X в диапазоне (0; 8).

1. Блок – схемы:

 

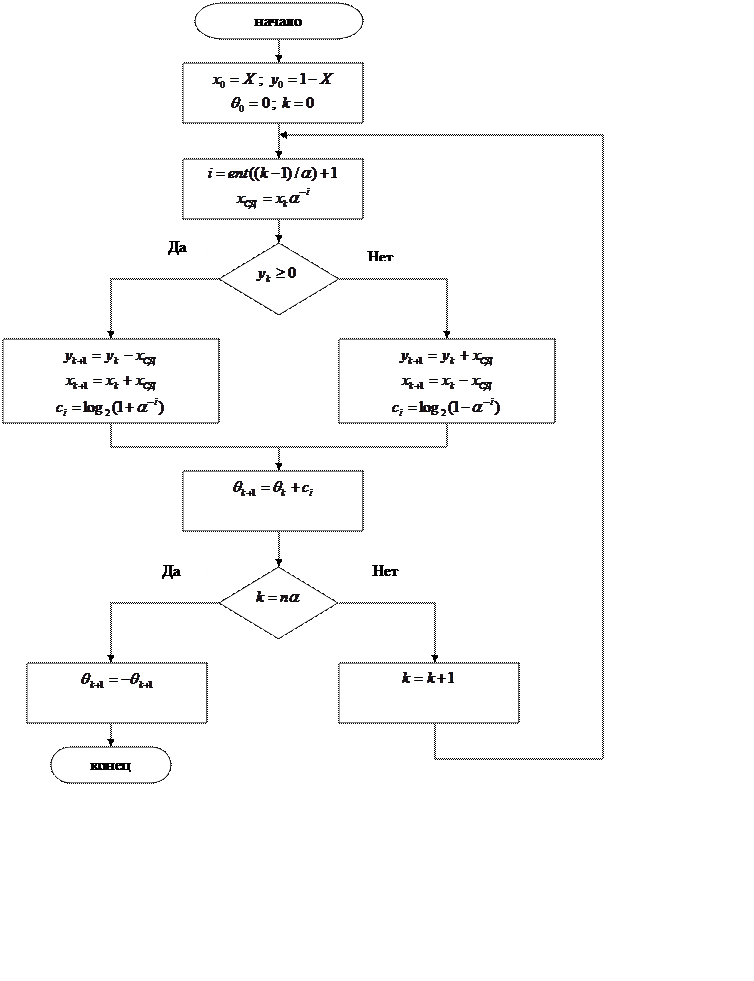Рисунок 2. Блок – схемы алгоритма вычисления

2. По этому алгоритму была написана программа:

#include <iostream.h>

#include <math.h>

int main(int argc, char* argv[])

{

float x[256],X,F[256],y[256],Xcd,c[255];

int a=2,k=-1,i,n=16;

F[0]=0;

cin >> X;

x[0]=X;

y[0]=1-X;

do

{

k=k+1;

i=((k-1)/a)+1;

Xcd=x[k]*pow(a,-i);

if (y[k] >=0) {    y[k+1]=y[k]-Xcd;

x[k+1]=x[k]+Xcd;

c[i]=log(1+pow(a,-i))/log(2);

}

else {                                  y[k+1]=y[k]+Xcd;

x[k+1]=x[k]-Xcd;

c[i]=log(1-pow(a,-i))/log(2);};

F[k+1]=F[k]+c[i];

}

while (k!=n*a);

F[k+1]=-F[k+1];

cout << F[k+1];

return 0;

}

5.                                Выбор варианта реализации.

Большую часть времени занимает вычисление выражение  (), которое производится при помощи i операции деления на 2 или i сдвигов вправо. Так как не задан критерий быстродействия, то можно воспользоваться сдвиговыми регистрами.

Для хранения входных и выходных значений используется формирователи (BFI и BFO, реализованные на двух КР1533АП14 D1– D2 и D3 – D4, соответственно)

Для хранения значения , , ,  используются регистры RGX, RGY, RGT, RGC, реализованные на двух КР1533ИР35 (D13– D14, D15 – D16, D36 – D37 и D38 – D39), для  используется сдвиговый регистр RGSX, реализованный на двух КР1533ИР13 (D27– D28). Для хранения значений i, k используются счетчики CTI, CTK. CTI реализован на одном КР1533ИЕ7 (D33), CTK на двух (D29– D30).

Операции сложения и вычитания могут быть реализованы на АЛУ посредством задания режима работы. Знаковый бит  управляет выбором режима. Таким образом, если  является положительным (RGY[15] = 0), то RGX складывается с RGSX, из RGY вычитается значение RGSX, иначе (RGY[15] = 1) из RGX вычитается  значение RGSX, а RGY складывается с RGSX. В схеме использованы 4 – ех разрядные АЛУ КР1533ИП3, со схемами ускоренного переноса КР1533ИП4 (SMX –17– D20, SMY – D21– D24 и ALUT – D41– D44).

Операции изменения знака могут быть заменены инвертированием всех разрядов и прибавление младшей единицы.

Для загрузки начальных значений в регистры используется мультиплексоры, во время выполнения итераций на мультиплексорах MXX  и  MXY выбран 0 – ой канал, во время инициализации (установки начальных значений  X  в регистры RGX, и 1 в RGY), реализованы на четырех КР1533КП14А (D5 – D8 и D9 – D12).

6.                                         Описание работы схемы:

1. Внешнее устройство устанавливает на шине данных аргумент и запускающий сигнал, который производит запуск управляющего автомата и сброс счетчика CTK и регистра RGT.