Проектирование принципиальной схемы процессора для вычисления функции log2(x) методом “цифра за цифрой”, страница 2

Различные табличные методы основаны большей частью на методах криволинейной или кусочно – линейной аппроксимации. Достоинством их является малое требуемое число арифметических операций, необходимых для вычисления функции. Однако практическое их использование ограничивается требованием большого объема запоминающего устройства. При табличном методе для вычисления только одной функции требуется в среднем 2^n/2 – 2ⁿ значений, что составляет для ЦВМ с 24 – разрядной сеткой, не менее 4096 ячеек памяти. Этот фактор ограничивает практическое применение рассматриваемого метода вычислительными машинами длиной слов, не превышающей 12 – 15 двоичных разрядов.

Сущность итерационных методов состоит в построение последовательности y_i+1 = f(y_i), сходящейся к функции y(x). Эффективность применения данного метода зависит, во-первых, от скорости сходимости (необходимого числа итераций, удовлетворяющей заданной точности), и, во-вторых, от набора операций, выполняющихся в каждом шаге. Необходимость в ряде случаев операций деления и умножения в процессе выполнения итераций существенно увеличивает время вычисления.

Наиболее часто используется метод полиноминальной аппроксимации, но в последнее время разработчиков вычислительных машин стал привлекать итерационный метод “цифра за цифрой”.

3.                                         Описание алгоритма:

Методом “цифра за цифрой” называется, итерационны вычислительный процесс, основные характеристики которого непосредственно зависят от основания используемой системы исчисления и от числа верных цифр, результата.

Техника применения метода состоит в разбиение процесса вычисления функции на два этапа. На обоих этапах строится итерационная последовательность:

где  - векторное поле, указывающее направление движения;  - положительный скаляр, показывающий длину шага итерации.

Начальным значением которой на первом этапе служит величина аргумента функции, представленного n – разрядной правильной дробью.

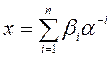
где  

пределом последовательности на данном этапе является постоянная величина с, равна 1 или 0. Результатом этого полученного набора значений . Если аргумент превышает единицу, то он может быть приведен к диапазону , с помощью масштабирования или формул приведения.

На втором этапе в качестве начального значения в зависимость от типа вычисляемой функции берется 0, 1 либо некоторая константа, соответствующая данной функции. На основании полученного, на первом этапе значения  строится итерационная последовательность, пределом которой служит значение вычисляемой функции.

Абсолютные значения величин шагов итерации  в методе “цифра за цифрой” ставится в соответствие некоторая величина i. Величина i в зависимости от типа вычислений принимает ряд целых значений  или . Приращение величины i на единицу можно поставить в зависимости от номера итерации k либо от изменения .

В первом случае величина  меняется через постоянное для данной функции число шагов – q и поэтому можно говорить о синхронной организации итерационного процесса. При этом окончание итерации происходит при достижении величины k значения , зависящей только от основания системы счисления , разрядности n и вида вычисления.

В случае  значение i на каждой итерации определяется из соотношения

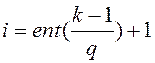
а в случае  

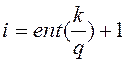
Если взять приращение значения i с изменение знака величины , то в этом случае количество итераций с постоянной величиной шага будет различным для каждого i, а итерации завершаются, если  окажутся не больше заданной величины. Это происходит при условии . Такую организацию итерационного процесса называют асинхронной.

При асинхронной организации приращение величины i на единицу производится всякий раз при смене знака . Если допустить что знаковая функция может принимать только два значения 1 и –1, то можно записать .

Значение  задается равным 0 – для прямых и обратных тригонометрических функций, или 1 – для прямых и обратных гиперболических функций.