Проектирование принципиальной схемы процессора для вычисления функции log2(x) методом “цифра за цифрой”

1.                                                             Задание:

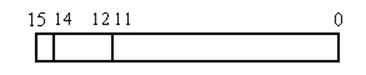
          Спроектировать принципиальную схему процессора для вычисления функции методом “цифра за цифрой”. Разрядная сетка процессора – 16 разряд с фиксированной запятой: 1 – знаковый разряд, 3 – разряда целая часть, 12 – разрядов дробная часть.

Рисунок 1. Формат представления числа с фиксированной запятой.

2.                                                             Введение.

На протяжении всей истории развития вычислительной техники очередной переход на новую элементарно – технологическую базу, позволяя уменьшить в первую очередь массогабаритные характеристики ЭВМ, резко повышал области их применения. Это в большинстве случаев приводило к тому, что возрастали требования к их быстродействию. Наиболее распространенным путем решения этой задачи является переход от универсальных средств вычислительной техники к специализированным средствам. Наиболее перспективным следует считать подход, состоящий в организации сочетании универсальных и специализированных средств.

Разработка специализированных процессоров, реализуемых на БИС, технически и экономически обоснована только при их достаточно широком применении. Это в свою очередь заставляет, во-первых, выделить класс типовых вычислительных задач, и, во-вторых, найти алгоритмы, обладающими широкими функциональными возможностями.

Из широкого круга задач, решаемы специализированными процессорами, в первую очередь можно выделить типовые вычислительные операции – вычисление элементарных функций, преобразование координат, векторные операции.

Работа специализированных процессоров, называемых также преобразователями или функциональными расширителями, основывается на ряде известных численных методов – полиномиальной и дробно – рациональной аппроксимации, кусочно – линейной и нелинейной интерполяции,  итерационных процессах.

Выбор метода и алгоритмов выполнения операций в специализированных процессорах всегда должен проводится с учетом используемой элементарной базы.

Существует большое количество разнообразных методов вычисления элементарных функций. Из них в цифровой вычислительной технике нашли применение:

1.  разложение в ряд Тейлора;

2.  аппроксимация с помощью различного вида полиномов наилучшего приближения;

3.  цепные дроби;

4.  рациональное приближение;

5.  табличные методы;

6.  итерационные методы.

Степенные полиномы (отрезок ряда Тейлора, полиномы Чебышева, …) вычисляется в ЦВМ чаще всего по схеме Горнера. Время, необходимое для вычисления полинома, при разложении функции произвольного вида, приблизительно равно

, где m – степень полинома; t_умн – время выполнения команды умножения; t_сл – время выполнения команды сложения.

Преимуществом разложения в ряд Тейлора является возможность вычисления коэффициентов членов ряда непосредственно в процессе работы. В связи с этим отсутствует необходимость запоминания их в памяти машины, как это требуется при полиномиальной аппроксимации по Чебышеву. Однако такой способ определения коэффициентов требует значительного времени вычисления. Недостатком использования ряда Тейлора является также его медленная сходимость при вычисление функций ln x, arctg x, arcsin x, сто приводит к большому времени вычисления и накопления значительной инструментальной погрешности. Кроме того, при этом способе методическая погрешность монотонно возрастает с увеличением аргумента. Для уменьшения влияние этого вида погрешности аргумент предварительно сводят в более узкую область с помощью соответствующих преобразований.

Методическая погрешность полиномиальной аппроксимации знакопеременна и равномерно распределена по промежутку изменения аргумента. К недостаткам этого вида метода следует отнести большую загрузку ПЗУ, в которое должны быть записаны коэффициенты всех аппроксимирующих полиномов.

Преимуществом цепных дробей является малый требуемый объем ПЗУ, принципиально более широкая область сходимости, чем для ряда Тейлора, и универсальность применения программы, вычисления цепной дроби для различных функций. Однако практически получается, что  при увеличении аргумента функции резко возрастает необходимое число звеньев дроби, что заставляет приводить аргументы к интервалу, не более широкому, чем при разложении в ряд Тейлора. Недостатком этого метода является, во-первых, необходимость наличие в системе команд машины операции деления, во-вторых, большое время вычисления, которое для даже самого быстрого способа составляет , где v – число звеньев дроби, зависящее от вида функции и требуемой точности; t_ц.др. – время реализации цепных дробей.

При использовании рациональных приближений элементарные функции представляются в виде отношений двух полиномов с числом членов в каждом намного меньшем, чем для соответствующих разложений в ряд Тейлора. Однако при данном методе все коэффициенты полиномов должны быть предварительно занесены в память. Время вычисления элементарной функции при использовании рациональных приближений состоит из суммарного времени вычисления двух полиномов и выполнения операции деления.