Центральная гироскопическая вертикаль типа ЦГВ, страница 3

Проведем исследования на основе прецессионных движений гиромаятника. Нутацию как составляющую движения не учитываем, так как в данном случае она не имеет практического значения.

Уравнения движения тяжелого гироскопа, ось OZ которого направлена по вертикали места (рис. 2), с учетом трения в осях карданового подвеса запишем в следующем виде:

или

где М_ТХ, М_TY - моменты трения в осях карданового подвеса:

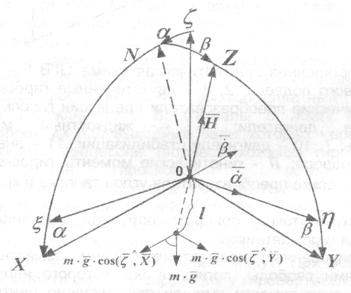
Рис. 2. Положение маятника по отношению к точке подвеса

Решение уравнений будет таким:

Траектория движения конца оси ротора на картинной плоскости, описанная уравнением , имеет вид, изображенный на рис. 3. Заметим, что конец оси ротора гироскопа приходит к вертикали места

с точностью углов застоя и , определяемых силами трения в осях карданового подвеса.

Дифференциальные уравнения тяжелого гироскопа с трением и коррекцией имеют вид:

где и  - моменты коррекции.

Траектория движения конца оси ротора на картинной плоскости, описанная уравнениями, показана на рис. 4.

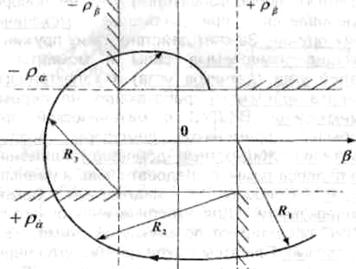
Рис.3. Траектория движения конца оси ротора на картинной плоскости

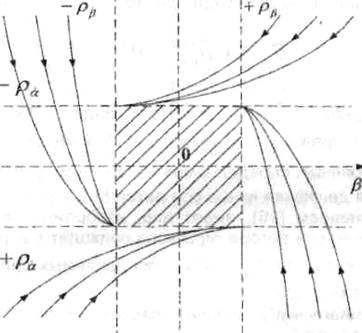
Рис. 4. Траектория движения конца оси ротора на картинной плоскости

Результат эксперимента:

Исследование статических характеристик ЦГВ по углам крена и тангажа