|
0 |
C3 |
C4 |
DA1 |
R7 |
R8 |
R9 |
VT2 |
B11 |
B12 |
|
C3 |
0 |
0 |
5 |
0 |
0 |
0 |
0 |
0 |
0 |
|
C4 |
0 |
0 |
5 |
0 |
0 |
0 |
0 |
0 |
0 |
|
DA1 |
5 |
5 |
0 |
40 |
0 |
0 |
0 |
0 |
0 |
|
R7 |
40 |
0 |
0 |
0 |
0 |
0 |
12,5 |
15 |
17,5 |
|
R8 |
0 |
0 |
0 |
0 |
0 |
0 |
2,5 |
0 |
0 |
|
R9 |
0 |
0 |
0 |
0 |
0 |
0 |
2,5 |
0 |
0 |
|
VT2 |
0 |
0 |
0 |
12,5 |
2,5 |
2,5 |
0 |
0 |
0 |
|
B11 |
0 |
0 |
0 |
15 |
0 |
0 |
0 |
0 |
2,5 |
|
B12 |
0 |
0 |
0 |
17,5 |
0 |
0 |
0 |
2,5 |
0 |
![]()
|
1 |
C3 |
C4 |
DA1 |
R7 |
R8 |
R9 |
VT2 |
B11 |
B12 |
|
C3 |
0 |
0 |
2,5 |
0 |
0 |
0 |
0 |
0 |
0 |
|
C4 |
0 |
0 |
2,5 |
0 |
0 |
0 |
0 |
0 |
0 |
|
DA1 |
2,5 |
2,5 |
0 |
2,5 |
0 |
0 |
0 |
0 |
0 |
|
R7 |
2,5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
R8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
R9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
VT2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
B11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
B12 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
![]() , L1-L0 = -95,
дальнейшее решение не целесообразно т.к. должно учитываться расстояние между микросхемой.
, L1-L0 = -95,
дальнейшее решение не целесообразно т.к. должно учитываться расстояние между микросхемой.
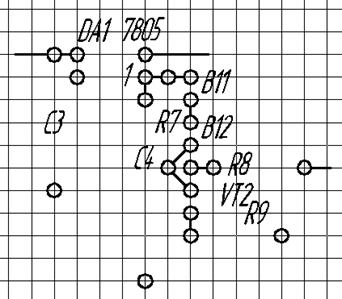
Матрица расстояний для 4 части:
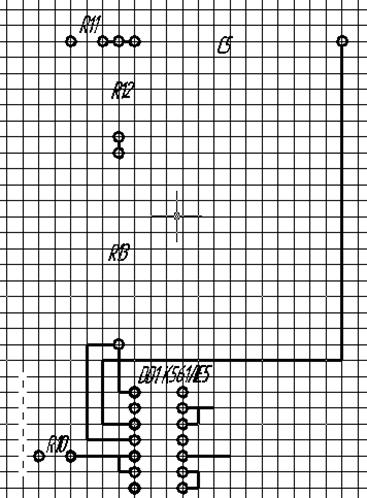
|
0 |
DD1 |
R10 |
R11 |
R12 |
R13 |
C5 |
|
DD1 |
0 |
7,5 |
0 |
0 |
10 |
120 |
|
R10 |
7,5 |
0 |
85 |
0 |
0 |
0 |
|
R11 |
0 |
85 |
0 |
2,5 |
0 |
0 |
|
R12 |
0 |
0 |
2,5 |
0 |
2,5 |
2,5 |
|
R13 |
10 |
0 |
0 |
2,5 |
0 |
0 |
|
C5 |
120 |
0 |
0 |
2,5 |
0 |
0 |
![]()
|
1 |
DD1 |
R10 |
R11 |
R12 |
R13 |
C5 |
|
DD1 |
0 |
2,5 |
0 |
0 |
2,5 |
2,5 |
|
R10 |
2,5 |
0 |
0 |
0 |
0 |
0 |
|
R11 |
0 |
0 |
0 |
0 |
0 |
0 |
|
R12 |
0 |
0 |
0 |
0 |
0 |
0 |
|
R13 |
2,5 |
0 |
0 |
0 |
0 |
0 |
|
C5 |
2,5 |
0 |
0 |
0 |
0 |
0 |
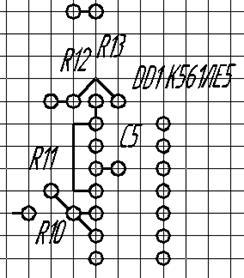
![]() , L1-L0 = -225,
дальнейшее решение не целесообразно т.к. должно учитываться расстояние между микросхемой.
, L1-L0 = -225,
дальнейшее решение не целесообразно т.к. должно учитываться расстояние между микросхемой.
2. Соединение схем при помощи последовательного алгоритма размещения.
Данный алгоритм не требует первоначального размещения элементов.
В основе этого алгоритма лежат критерии минимизации длины самой длинной связи, вследствие чего и критерий максимума числа связей между модулями находящимися в соседних позициях.
Алгоритм заключается в том, что идет расположение элементов на печатной плате в зависимости от количества связей этого элемента с другими, что позволяет уменьшить длину связей.
Первый элемент следует выбирать с большим количеством связей и располагать его в центре печатной плате.
Матрица связей.
|
1 |
2 |
3 |
4 |
|
|
1 |
0 |
1 |
0 |
1 |
|
2 |
1 |
0 |
1 |
1 |
|
3 |
0 |
1 |
0 |
1 |
|
4 |
1 |
1 |
1 |
0 |
Максимальное количество связей у 4 части, следовательно, выберем его в качестве первого и расположим в центре печатной платы.
Далее будем выбирать элементы с большим количеством связей и располагать их на печатной плате, так чтобы длина связей была минимальна.
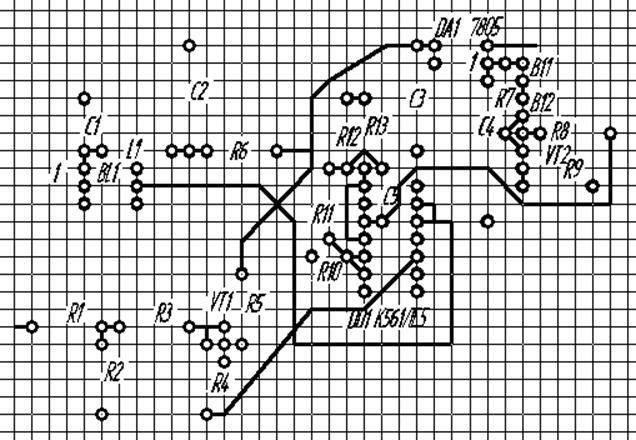 В
итоге получили оптимальное расположение элементов на печатной плате.
В
итоге получили оптимальное расположение элементов на печатной плате.
Вывод: В ходе данной работы была оптимизирована схема при помощи двух алгоритмов (перестановка и последовательное размещение). В ходе работы были допущены упрощения, т.е. без трассировки, вследствие чего данная схема требует доработки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.