|
C3 |
C4 |
DA1 |
R7 |
R8 |
R9 |
VT2 |
B11 |
B12 |
|
|
C3 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
C4 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
DA1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
R7 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
|
R8 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
R9 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
VT2 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
B11 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
|
B12 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
DD1 |
R10 |
R11 |
R12 |
R13 |
C5 |
|
|
DD1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
R10 |
1 |
0 |
1 |
0 |
0 |
0 |
|
R11 |
0 |
1 |
0 |
1 |
0 |
0 |
|
R12 |
0 |
0 |
1 |
0 |
1 |
1 |
|
R13 |
1 |
0 |
0 |
1 |
0 |
0 |
|
C5 |
1 |
0 |
0 |
1 |
0 |
0 |
В основе алгоритма использующего перестановку элементов положен критерий минимизации суммарной длины всех связей между модулями.
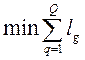 , где Q
–полное количество соединений.
, где Q
–полное количество соединений.
Смысл данного критерия заключается в том, что кратчайшие проводники занимаю меньшее число дискретных элементов печатной платы.
Алгоритм на каждом этапе вычисляет приращение суммарной длины связей на печатной плате для всех возможных попарных перестановок модулей.
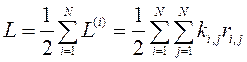 - суммарная длина всех
связей, где ki,j – матрица связей, а ri,j – матрица расстояний между точками на плате, в которых
размещены модули.
- суммарная длина всех
связей, где ki,j – матрица связей, а ri,j – матрица расстояний между точками на плате, в которых
размещены модули.
Для определения эффективного размещения элементов следует сравнить два L, рсачитанных при разных расположениях элементов, если их отношение L1-L0 является положительным числом, то это изменение положений элементов является не эффективным, т.к. приводит к увлечению длины связи. Тогда результат, полученный ранее, является оптимальным.
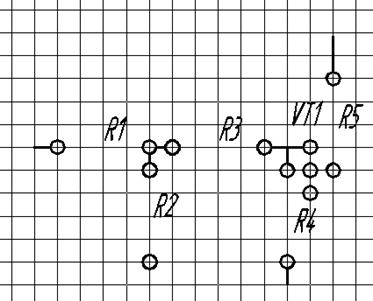
Зададим начальное положение элементов и расстояние между ними.
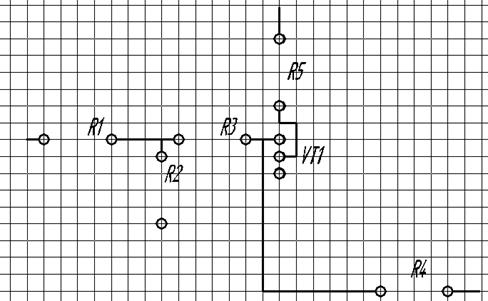
Матрица расстояний.
|
0 |
R1 |
R2 |
R3 |
R4 |
R5 |
VT1 |
|
R1 |
0 |
10 |
10 |
0 |
0 |
0 |
|
R2 |
10 |
0 |
0 |
0 |
0 |
0 |
|
R3 |
10 |
0 |
0 |
0 |
0 |
5 |
|
R4 |
0 |
0 |
0 |
0 |
0 |
40 |
|
R5 |
0 |
0 |
0 |
0 |
0 |
12,5 |
|
VT1 |
0 |
0 |
5 |
40 |
12,5 |
0 |
|
1 |
R1 |
R2 |
R3 |
R4 |
R5 |
VT1 |
|
R1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
R2 |
0 |
0 |
0 |
0 |
0 |
0 |
|
R3 |
0 |
0 |
0 |
0 |
0 |
0 |
|
R4 |
0 |
0 |
0 |
0 |
0 |
0 |
|
R5 |
0 |
0 |
0 |
0 |
0 |
0 |
|
VT1 |
0 |
0 |
0 |
0 |
0 |
0 |
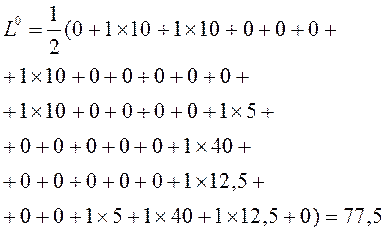
![]()
L1-L0 = -77, Такой результат можно объяснить тем, что используются только маломощные аналоговые элементы, вследствие чего расстояние между ними может стремится к 0;
Т.е. существует возможность использовать одно монтажное отверстие для нескольких элементов.
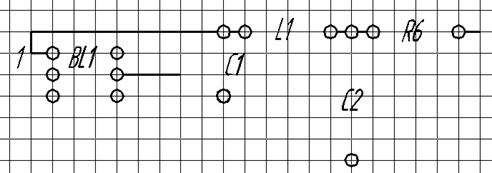
Матрица расстояний для 2 части.
|
0 |
BL1 |
C1 |
C2 |
L1 |
R6 |
|
BL1 |
0 |
27,5 |
0 |
0 |
0 |
|
C1 |
27,5 |
0 |
0 |
5 |
0 |
|
C2 |
0 |
0 |
0 |
5 |
5 |
|
L1 |
0 |
5 |
5 |
0 |
0 |
|
R6 |
0 |
0 |
5 |
0 |
0 |
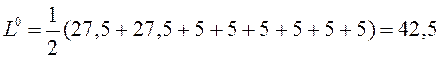
|
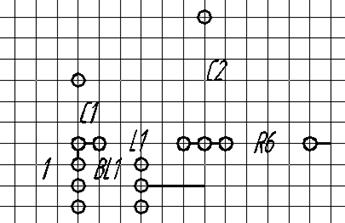
0 |
BL1 |
C1 |
C2 |
L1 |
R6 |
|
BL1 |
0 |
2,5 |
0 |
0 |
0 |
|
C1 |
2,5 |
0 |
0 |
0 |
0 |
|
C2 |
0 |
0 |
0 |
0 |
0 |
|
L1 |
0 |
0 |
0 |
0 |
0 |
|
R6 |
0 |
0 |
0 |
0 |
![]() , L1-L0 = -40,
дальнейшее решение не целесообразно т.к. должно учитываться расстояние между микросхемой.
, L1-L0 = -40,
дальнейшее решение не целесообразно т.к. должно учитываться расстояние между микросхемой.
Матрица расстояний для 3 части.

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.