Анализ на чувствительность поверхностной силы сжатия на конусную поверхность гвоздя

1 Индивидуальное задание

Результирующая формула                       σ =(R₃*E_der)/l_der [Н/м²]

где             σ – поверхностная сила сжатия на конусную поверхность гвоздя

R₃ – условный радиус закругления конуса острия гвоздя

E_der – модуль упругости дерева

l_der – максимальное расстояние, которое допустимо для данной породы дерева, при котором при извлечении гвоздя структура дерева восстанавливается.

R₃= 15*10^-6 м

E_der=10⁶ Па

l_der=0,2 м

Задача курсовой работы: получить анализ на чувствительность поверхностной силы сжатия на конусную поверхность гвоздя. Один параметр меняется,  остальные параметры заморожены. Диапазон изменения параметра ± 50% от заданного значения с шагом 10%.

2 Моделирование

2.1 Вариации входной переменной l_der

l_der–максимальное расстояние, которое допустимо для данной породы дерева, при котором при извлечении гвоздя структура дерева восстанавливается.

Вычисление шага моделирования :          Δl_der=(0,5* l_der)/5

Δl_der=(0,5* 0,2)/5=0,02

Диапазон изменения параметра l_der ± 50% от заданного значения с шагом 10%. Исходное значение исследуемого параметра l_der=0,2 м

Подставляем полученные значения изменяемого параметра в исходную формулу, оставляя остальные параметры заданными по условию, и вычисляем значение исследуемой величины от этих значений соответственно:

l_{der  n}=l_der +n*Δl_der                                       

l_{der  -5}=0,2-5*0,02=0,1                                 [м]

l_{der  -4}=0,2-4*0,02=0,12                               [м]

l_{der  -3}=0,2-3*0,02=0,14                               [м]

l_{der  -2}=0,2-2*0,02=0,16                               [м]

l_{der  -1}=0,2-1*0,02=0,18                               [м]

l_{der  0}=0,2-0*0,02=0,2                                 [м]

l_{der  +1}=0,2+1*0,02=0,22                                       [м]

l_{der  +2}=0,2+2*0,02=0,24                                       [м]

l_{der  +3}=0,2+3*0,02=0,26                                       [м]

l_{der  +4}=0,2+4*0,02=0,28                                       [м]

l_{der  +5}=0,2+4*0,02=0,3                               [м]

σ (l_{der  -5})=( 15*10^-6 *10⁶)/0,1=150             [Н/м²]

σ (l_{der  -4})=(15*10^-6 *10⁶)/0,12=125            [Н/м²]

σ (l_{der  -3})=(15*10^-6 *10⁶)/0,14=107,143     [Н/м²]

σ (l_{der  -2})=(15*10^-6 *10⁶)/0,16=93,75                   [Н/м²]

σ (l_{der  -1})=(15*10^-6 *10⁶)/0,18=83,333       [Н/м²]

σ (l_{der  0})=(15*10^-6 *10⁶)/0,2=75                 [Н/м²]

σ (l_{der  +1})=(15*10^-6 *10⁶)/0,22=68,182       [Н/м²]

σ (l_{der  +2})=(15*10^-6 *10⁶)/0,24=62,5           [Н/м²]

σ (l_{der  +3})=(15*10^-6 *10⁶)/0,26=57,692       [Н/м²]

σ (l_{der  +4})=(15*10^-6 *10⁶)/0,28=53,571       [Н/м²]

σ (l_{der  +5})=(15*10^-6 *10⁶)/0,3=50                [Н/м²]

По полученным значениям строим график зависимости поверхностной силы сжатия на конусную поверхность гвоздя от максимального расстояния, которое допустимо для данной породы дерева, при котором при извлечении гвоздя структура дерева восстанавливается.

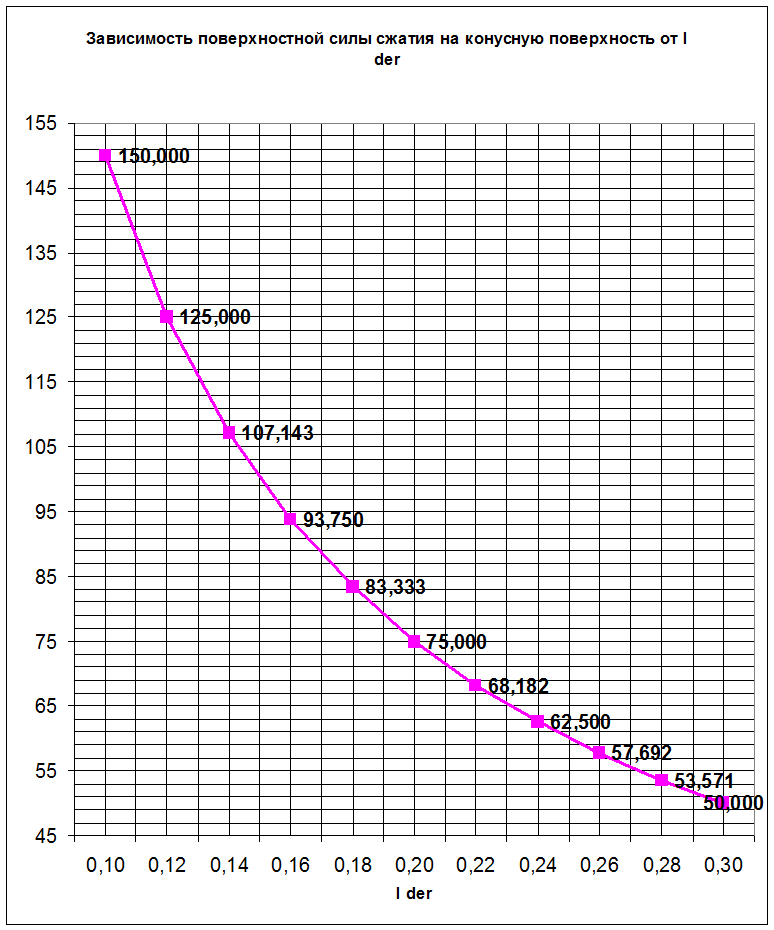
Определим наиболее чувствительный участок графика зависимости поверхностной силы сжатия на конусную поверхность гвоздя от максимального расстояния, которое допустимо для данной породы дерева, при котором при извлечении гвоздя структура дерева восстанавливается. Найдем коэффициент крутизны по формуле:

k _кр. = ∆y/∆x

k _кр.1 = 150-125 /0.3-0.12=138.88

k _кр.2 = 125-107.143 / 0.3-0.14=111.606

k _кр.3 = 107.143-93.75 / 0.3-0.16=95.664

k _кр.4 = 93.75-83.333 / 0.3-0.18=86.808

k _кр.5 = 83.333-75 / 0.3-0.2=83.33

k _кр.6 = 75-68.182 / 0.3-0.22=8.5225

k _кр.7 = 68.182-62.50 / 0.3-0.24=9.47

k _кр.8 = 62.50-57.692 / 0.3-0.26=12.02

k _кр.9 = 57.692-53.571 / 0.3-0.28=20.605

Вывод: при увеличении максимального расстояния, которое допустимо для данной породы дерева, при котором при извлечении гвоздя структура дерева восстанавливается, поверхностная сила сжатия на конусную поверхность гвоздя уменьшается в обратно пропорциональной зависимости.

2.2 Вариации входной переменной R₃

R₃– условный радиус закругления конуса острия гвоздя