Другие предметы \ Векторный анализ элементов систем управления

Анализ на чувствительность поверхностной силы сжатия на конусную поверхность гвоздя, страница 2

Вычисление шага моделирования: Δ R3=(0,5* R3)/5

Δ R3=(0,5* 15*10-6)/5=1,5*10-6

Диапазон изменения параметра R3 ± 50% от заданного значения с шагом 10%. Исходное значение исследуемого параметра R3= 15*10-6 м

Подставляем полученные значения изменяемого параметра в исходную формулу, оставляя остальные параметры заданными по условию, и вычисляем значение исследуемой величины от этих значений соответственно:

R3  n= R3+n*Δ R3

R3  -5=15*10-6-5*1,5*10-6=7,5*10-6            [м]

R3  -4=15*10-6-4*1,5*10-6=9*10-6               [м]

R3  -3=15*10-6-3*1,5*10-6=10,5*10-6                    [м]

R3  -2=15*10-6-2*1,5*10-6=12*10-6             [м]

R3  -1=15*10-6-1*1,5*10-6=13,5*10-6                    [м]

R3  0=15*10-6-0*1,5*10-6=15*10-6              [м]

R3  +1=15*10-6+1*1,5*10-6=16,5*10-6         [м]

R3  +2=15*10-6+2*1,5*10-6=18*10-6            [м]

R3  +3=15*10-6+3*1,5*10-6=19,5*10-6         [м]

R3  +4=15*10-6+4*1,5*10-6=21*10-6            [м]

R3  +5=15*10-6+4*1,5*10-6=22,5*10-6         [м]

σ (R3  -5)=(7,5*10-6 *106)/0,2=37,5             [Н/м2]

σ (R3  -4)=(9*10-6 *106)/0,2=45                   [Н/м2]

σ (R3  -3)=(10,5*10-6 *106)/0,2=52,5           [Н/м2]

σ (R3  -2)=(12*10-6 *106)/0,2=60                 [Н/м2]

σ (R3  -1)=(13,5*10-6 *106)/0,2=67,5           [Н/м2]

σ (R3  0)=(15*10-6 *106)/0,2=75                  [Н/м2]

σ (R3  +1)=(16,5*10-6 *106)/0,2=82,5          [Н/м2]

σ (R3  +2)=(18*10-6 *106)/0,2=90                [Н/м2]

σ (R3  +3)=(19,5*10-6 *106)/0,2=97,5          [Н/м2]

σ (R3  +4)=(21*10-6 *106)/0,2=105              [Н/м2]

σ (R3  +5)=(22,5*10-6 *106)/0,2=112,5        [Н/м2]

По полученным значениям строим график зависимости поверхностной силы сжатия на конусную поверхность гвоздя от условного радиуса закругления конуса острия гвоздя.

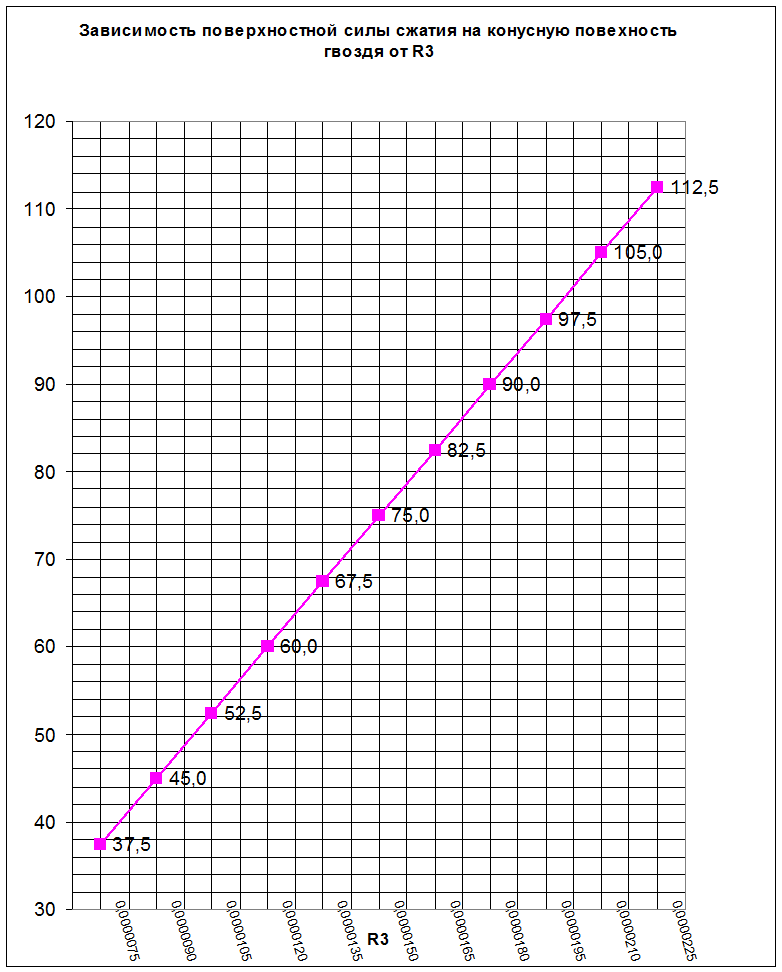
Вывод: при увеличении условного радиуса закругления конуса острия   гвоздя, поверхностная силы сжатия на конусную поверхность гвоздя увеличивается в прямо пропорциональной зависимости.

2.3 Вариации входной переменной Eder

Eder–модуль упругости дерева.

Вычисление шага моделирования: Δ Eder =(0,5* Eder)/5

Δ Eder =(0,5* 10*105)/5=1*105

Диапазон изменения параметра Eder ± 50% от заданного значения с шагом 10%. Исходное значение исследуемого параметра Eder=106 Па

Подставляем полученные значения изменяемого параметра в исходную формулу, оставляя остальные параметры заданными по условию, и вычисляем значение исследуемой величины от этих значений соответственно:

Eder  n= Eder +n*Δ Eder

Eder  -5=10*105-5*1*105=5*105                   [Па]

Eder  -4=10*105-4*1*105=6*105                   [Па]

Eder  -3=10*105-3*1*105=7*105                   [Па]

Eder  -2=10*105-2*1*105=8*105                   [Па]

Eder  -1=10*105-1*1*105=9*105                   [Па]

Eder  0=10*105-0*1*105=10*105                  [Па]

Eder  +1=10*105+1*1*105=11*105               [Па]

Eder  +2=10*105+2*1*105=12*105               [Па]

Eder  +3=10*105+3*1*105=13*105               [Па]

Eder  +4=10*105+4*1*105=14*105               [Па]

Eder  +5=10*105+4*1*105=15*105               [Па]

σ (Eder  -5)=(15*10-6*5*105)/0,2=37,5         [Н/м2]

σ (Eder  -4)=(15*10-6*6*105)/0,2=45            [Н/м2]

σ (Eder  -3)=(15*10-6 *7*105)/0,2=52,5        [Н/м2]

σ (Eder  -2)=(15*10-6*8*105)/0,2=60            [Н/м2]

σ (Eder  -1)=(15*10-6 *9*105)/0,2=67,5        [Н/м2]

σ (Eder  0)=(15*10-6 *10*105)/0,2=75                    [Н/м2]

σ (Eder  +1)=(15*10-6 *11*105)/0,2=82,5      [Н/м2]

σ (Eder  +2)=(15*10-6 *12*105)/0,2=90         [Н/м2]

σ (Eder  +3)=(15*10-6 *13*105)/0,2=97,5      [Н/м2]

σ (Eder  +4)=(15*10-6 *14*105)/0,2=105       [Н/м2]

σ (Eder  +5)=(15*10-6 *15*105)/0,2=112,5    [Н/м2]

По полученным значениям строим график зависимости поверхностной силы сжатия на конусную поверхность гвоздя от модуля упругости дерева.

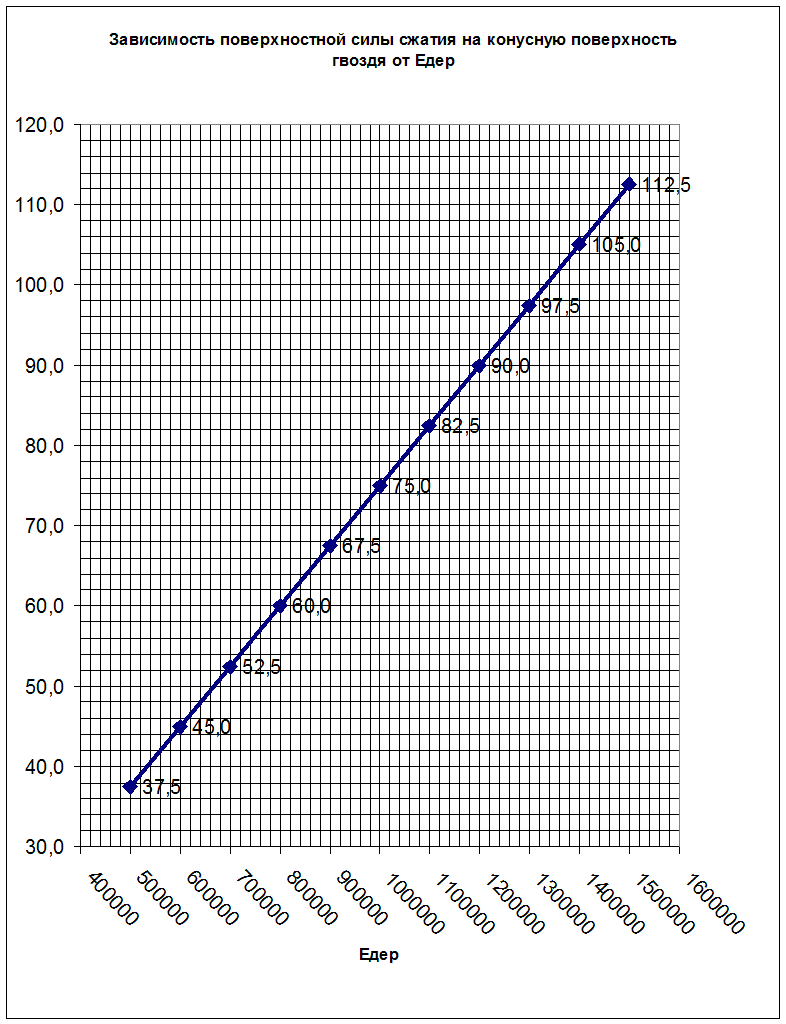
Вывод: при увеличении модуля упругости дерева, поверхностная силы сжатия на конусную поверхность гвоздя увеличивается в прямо пропорциональной зависимости.

Скачать файл