Изучение интегральной мощности диссипации при сжатии гвоздя

1. Индивидуальное задание:

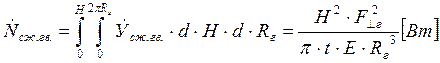
Интегральная мощность диссипации при сжатии гвоздя.

d = 4 мм = 0,004 м;

R_г = = 0,002 м;

R_г³ = = 0,002³ = 8· 10^{-9 м;}

H = 50 мм = 0,05 м;

E = Па

F_уд = 200 Н;                                                                          

β = 20º

β =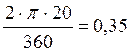рад

F = F_удН;

E = 200 Н·рад;

t_сек = 0,5 с;

d – диаметр гвоздя;

R_г – радиус  гвоздя;

H – длина гвоздя без шляпки;

E – модуль упругости материала гвоздя;

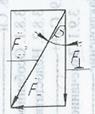
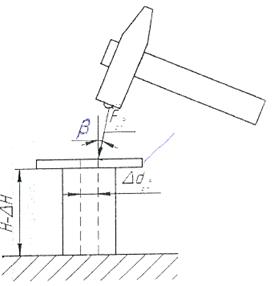
F - нормальная составляющая удара молотком по гвоздю, то есть сила, которая загоняет гвоздь в поверхность;

t_сек – время удара молотком по гвоздю;

β – пьяный угол.

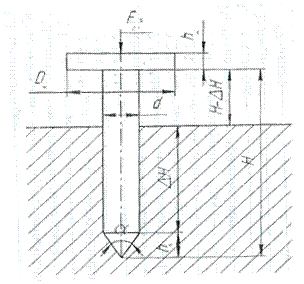
Задача курсовой работы:

Исследовать интегральную мощность диссипации при сжатии гвоздя. Один параметр меняется,  остальные параметры заморожены. Диапазон изменения параметра ± 50% от заданного значения с шагом 10%.

2. Моделирование.

2.1 Вариации входной переменной H

Вычисление шага моделирования:          

ΔH =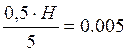

Диапазон изменения параметра H ± 50% от заданного значения с шагом 10%.

ΔH _-5 = H – 5ΔH = 0,05 - 0,025 = 0,025;

ΔH _-4 = H – 4ΔH = 0,05 – 0,02 = 0,03;

ΔH _-3 = H –3ΔH = 0,05 – 0,015 = 0,035;

ΔH _-2 = H – 2ΔH = 0,05 – 0,01 =  0,04;

ΔH _-1 = H – ΔH = 0,05 – 0,005 = 0,045;

ΔH ₀ = H – 0ΔH = 0,05 – 0 = 0,05;

ΔH ₊₁ = H + ΔH = 0,05 + 0,005 = 0,055;

ΔH ₊₂ = H + 2ΔH = 0,05 + 0,01 =  0,06;

ΔH ₊₃ = H +3ΔH = 0,05 + 0,015 = 0,065;

ΔH ₊₄ = H + 4ΔH = 0,05 + 0,02 = 0,07;

ΔH ₊₅ = H + 5ΔH = 0,05 + 0,025 = 0,075.

Подставляем полученные значения изменяемого параметра в исходную формулу, оставляя остальные параметры исходными, и вычисляем значение исследуемой формулы от этих значений соответственно:

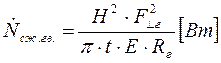
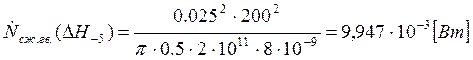
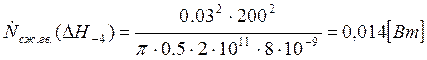
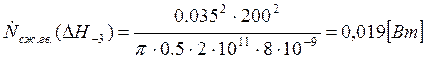
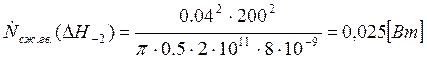
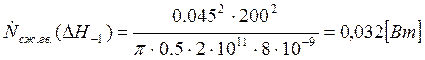
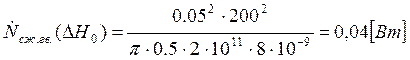
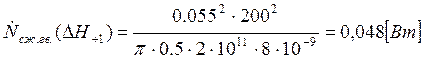
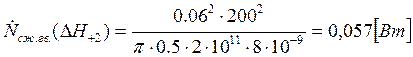
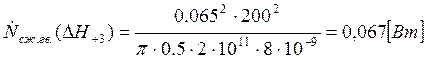
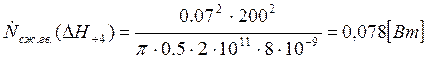
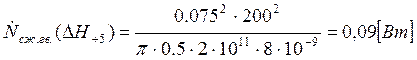
По полученным значениям строим график зависимости интегральной мощности диссипации при сжатии гвоздя от длины гвоздя без шляпки.

Вывод: при увеличении длины гвоздя интегральная мощность диссипации при сжатии гвоздя увеличивается.

2.2 Вариации входной переменной

β = 20º

Переводим угол β в радианы:

β =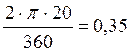рад

cos (0.35) ≈ 1

F_уд = 200 Н

Вычисление шага моделирования:          

Δ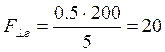

Диапазон изменения параметра  ± 50% от заданного значения с шагом 10%.

Δ

Δ

Δ 

Δ

Δ

Δ

Δ

Δ

Δ

Δ

Δ

Подставляем полученные значения изменяемого параметра в исходную формулу, оставляя остальные параметры исходными, и вычисляем значение исследуемой формулы от этих значений соответственно:

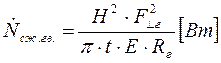
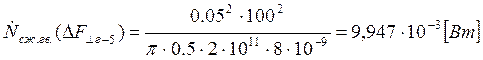
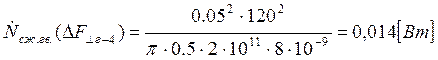
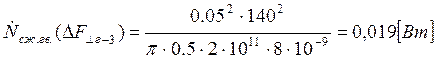
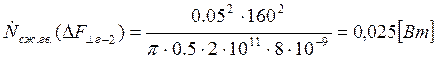
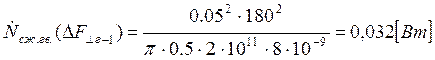
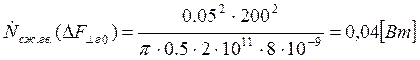
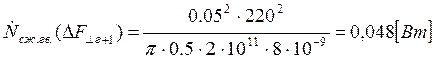
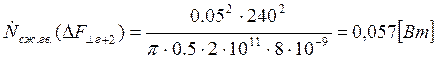
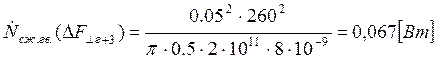
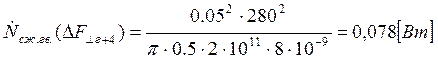
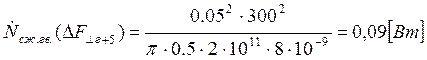
По полученным значениям строим график зависимости интегральной мощности диссипации при сжатии гвоздя от нормальной составляющей удара молотком по гвоздю.

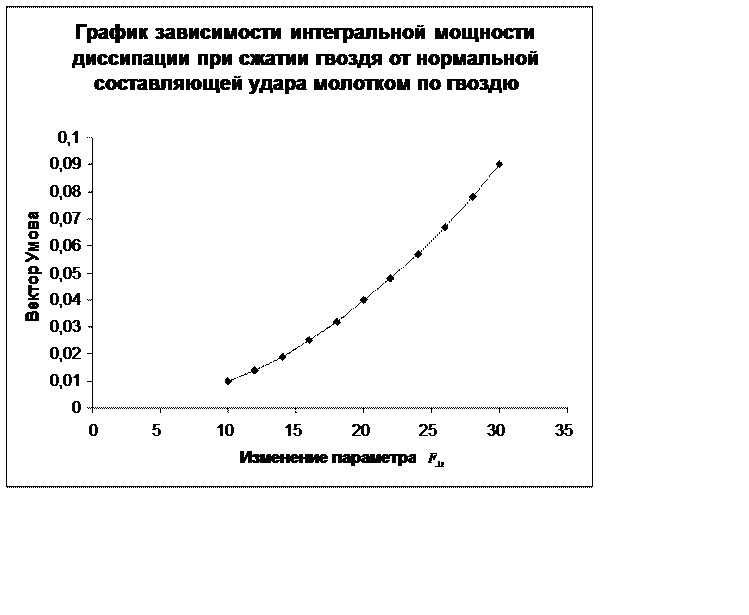
Вывод: интегральная мощность диссипации при сжатии гвоздя увеличивается при увеличении силы, которая загоняет гвоздь в поверхность.

2.3 Вариации входной переменной t = 0.5 c

Вычисление шага моделирования:          

Δt =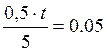

Диапазон изменения параметра t ± 50% от заданного значения с шагом 10%.

Δt _-5 = t – 5Δt = 0,5 – 0,2 5 = 0,25;

Δt _-4 = t – 4Δt = 0,5 – 0,2 = 0,3;

Δt _-3 = t – 3Δt = 0,5 – 0,1 5 = 0,35;

Δt _-2 = t – 2Δt = 0,5 – 0,1 = 0, 4;

Δt _-1 = t – Δt = 0,5 – 0,05 = 0, 45;

Δt ₀ = t + Δt = 0,5 + 0·0,05 = 0,5;

Δt ₊₁ = t + Δt = 0,5 + 0,05 = 0, 55;

Δt ₊₂ = t + 2Δt = 0,5 + 0,1 = 0,6;

Δt ₊₃ = t + 3Δt = 0,5 + 0,1 5 = 0,6 5;

Δt ₊₄ = t + 4Δt = 0,5 + 0,2 = 0,7;

Δt ₊₅ = t + 5Δt = 0,5 + 0,2 5 = 0,7 5.

Подставляем полученные значения изменяемого параметра в исходную формулу, оставляя остальные параметры исходными, и вычисляем значение исследуемой формулы от этих значений соответственно:

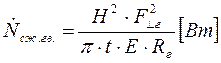
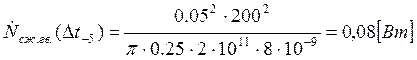
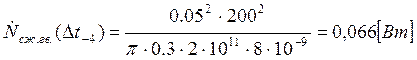
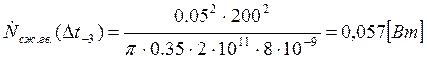
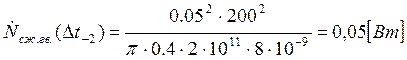
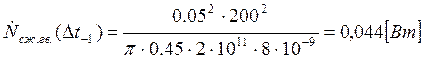
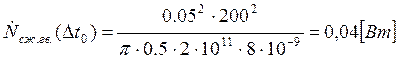
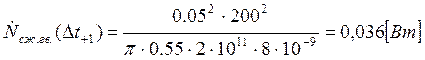
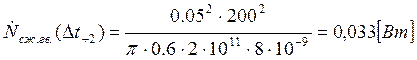
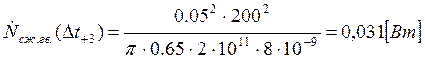
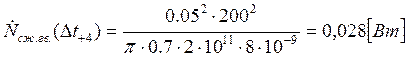
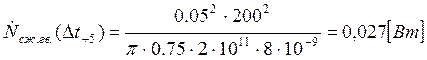
По полученным значениям строим график зависимости интегральной мощности диссипации при сжатии гвоздя от времени удара молотком по гвоздю.

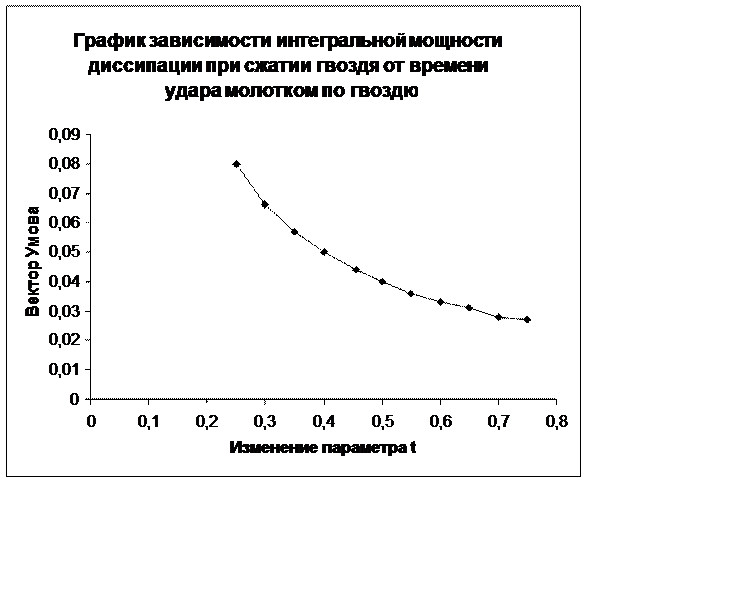
Вывод: при увеличении времени удара молотком по гвоздю  интегральная мощность диссипации при сжатии гвоздя уменьшается.

2.4 Вариации входной переменной E = Па

Вычисление шага моделирования:          

ΔE =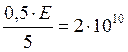

Диапазон изменения параметра Е ± 50% от заданного значения с шагом 10%.

ΔE _-5 = E – 5ΔE =

ΔE _-4 = E – 4ΔE =  

ΔE _-3 = E – 3ΔE =

ΔE _-2 = E – 2ΔE =

ΔE _-1 = E – ΔE =

ΔE ₀ = E – 0ΔE =

ΔE ₊₁ = E + ΔE =

ΔE ₊₂ = E + 2ΔE =

ΔE ₊₃ = E + 3ΔE =

ΔE ₊₄ = E + 4ΔE =

E ₊₅ = E + 5ΔE =

Подставляем полученные значения изменяемого параметра в исходную формулу, оставляя остальные параметры исходными, и вычисляем значение исследуемой формулы от этих значений соответственно:

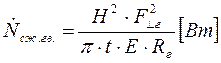
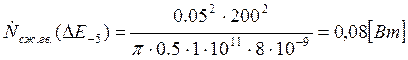
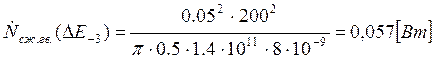
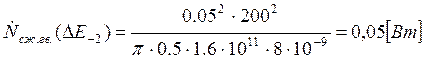
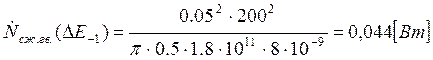
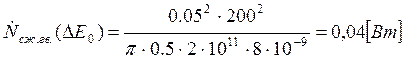
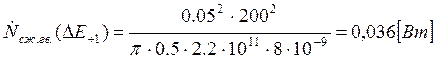
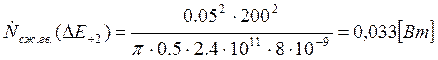
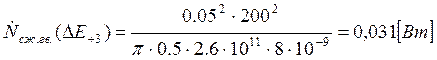
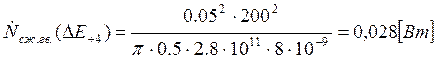
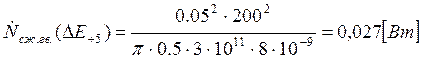
По полученным значениям строим график зависимости интегральной мощности диссипации при сжатии гвоздя от модуля упругости материала гвоздя.

Вывод: при увеличении модуля упругости материала гвоздя интегральная мощность диссипации при сжатии гвоздя уменьшается.

2.5 Вариации входной переменной R_г =

d = 4 мм = 0,004 м

R_г =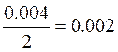

Вычисление шага моделирования:          

ΔR_г =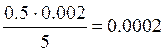

Диапазон изменения параметра H ± 50% от заданного значения с шагом 10%.

ΔR_{г -5} = R_г – 5ΔR_г = 0,002 – 0,001 =

ΔR_{г -4} = R_г – 4ΔR_г = 0,002 – 0,0008 =

ΔR_{г -3} = R_г – 3ΔR_г = 0,002 – 0,0006 =

ΔR_{г -2} = R_г – 2ΔR_г = 0,002 – 0,0004 =

ΔR_{г -1} =  R_г – ΔR_г = 0,002 – 0,0002 =

ΔR_{г 0} =  R_г – 0ΔR_г = 0,002 – 0 =

ΔR_{г +1} =  R_г + ΔR_г = 0,002 + 0,0002 =

ΔR_{г +2} = R_г + 2ΔR_г = 0,002 + 0,0004 =

ΔR_{г +3} = R_г + 3ΔR_г = 0,002 + 0,0006 =

ΔR_{г +4} = R_г + 4ΔR_г = 0,002 + 0,0008 =

ΔR_{г +5} = R_г + 5ΔR_г = 0,002 + 0,001 =

Подставляем полученные значения изменяемого параметра в исходную формулу, оставляя остальные параметры исходными, и вычисляем значение исследуемой формулы от этих значений соответственно:

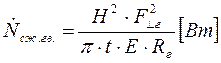
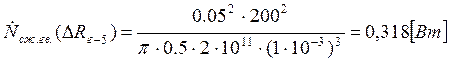
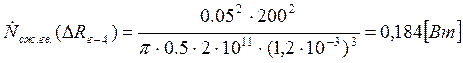
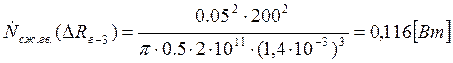
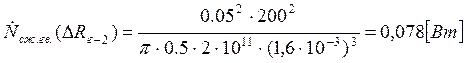
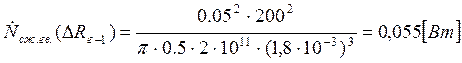
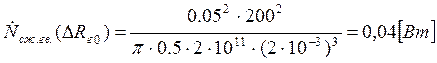
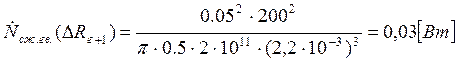
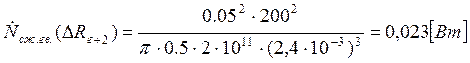
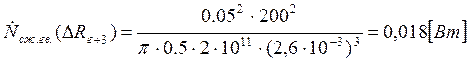
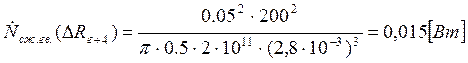
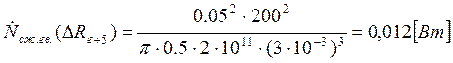
По полученным значениям строим график зависимости интегральной мощности диссипации при сжатии гвоздя от радиуса гвоздя.

Вывод: интегральная мощность