Ответы на экзаменационные вопросы № 1-46 по дисциплине "Физика" (Взаимодействие зарядов. Закон Кулона. Квазистационарное электромагнитное поле. Колебательный контур)

Экзаменационные вопросы по физике, часть 2

1. Взаимодействие зарядов. Закон Кулона. Электрическое поле, напряженность электрического поля. Принцип суперпозиции.

Взаимодействие точечных зарядов.

Точечным зарядом называется заряженное тело, размерами которого можно пренебречь, по сравнению с расстояниями, на которых рассматривается воздействие этого тела на другие заряженные тела.  Сила взаимодействия F между двумя точечны-ми зарядами q₁ и q₂ пропорциональна произведению величин зарядов q₁ и q₂ и обратно  пропорциональна квадрату расстояния r между ними:

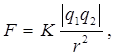
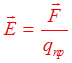Отношение силы    , действующей на пробный заряд со стороны поля к величине пробного заряда q_пр    определяет физическую величину, называемую напряженностью электростатического поля :

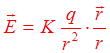
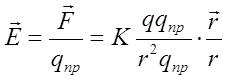
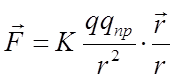Напряженность электростатического поля в некоторой точке является фи-зической величиной, численно равной силе, действующей на единицу поло-жительного заряда, помещенного в эту точку, и имеющей направление этой силы

 

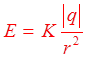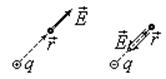Вектор     во всех точках поля направлен  радиально от заряда, если он положителен,  и радиально к заряду, если отрицателен.

Принцип суперпозиции полей

Электрическое поле каждого заряда не зависит от существования элек-трических полей других зарядов. Эти поля, накладываясь (друг на дру-га), создают результирующее поле, напряженность которого равна век-торной сумме напряженностей по-лей, создаваемых каждым зарядом в отдельности  а потенциал результирующего поля равен алгебраической сумме потенциалов этих полей          

Если необходимо найти напряженность и потенциал поля заряженного тела больших размеров, то это тело нужно разбить на такие малые участки, чтобы каждый участок можно было считать точечным зарядом.

 

2.  Поток вектора-напряженности электрического поля. Теорема Остроградского-Гаусса и ее применение для расчета полей заряженных плоскости, цилиндра и сферы.

Поток вектора    Е электрического поля     через поверхность S измеряетсячислом силовых линий пронизывающих данную поверхность.

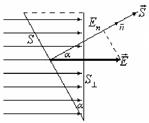
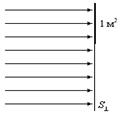В случае однородного поля, перпендикулярного к  плоской поверхности         число линий, пронизывающих 1 м²                                   равно  Е , а           через всю  поверхность  S_┴     поток вектора напряженности будет равен

 

Потоки через поверхности  S и S_┴ одинаковы. Так как                               то

       есть проекция вектора   Е   на направление нормали к поверхности S.  В этом случае

Введем понятие вектора площади         сонаправленного с единичным вектором       нормали к поверхности S , а по модулю равного площади этой поверхности

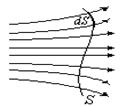
Тогда поток через поверхность будет равен

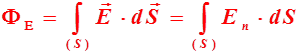
В случае  неоднородного поля       и произвольной     поверхности S 

Теорема гаусса

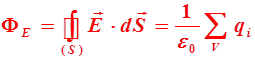
Поток вектора напряжённости электрического поля через любую замкнутую поверхность равен алгебраической сумме зарядов,  находящихся внутри объёма ограниченного  этой поверхностью делённой на электрическую постоянную       :   

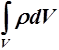
При непрерывном распределении заряда теорема Гаусса принимает вид

Где                   — есть заряд, находящийся внутри объёма, ограниченного замкнутой поверхностью S.

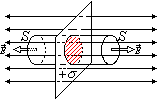
Поле бесконечной, равномерно заряженной плоскости

 

 

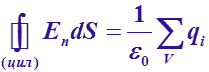
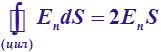
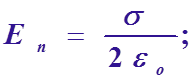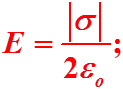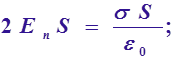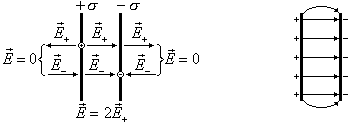Поле двух плоскостей

 

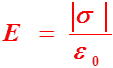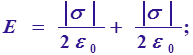Поле бесконечно длинного заряженного цилиндра (нити)

 

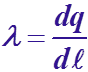
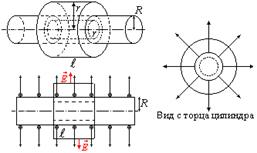
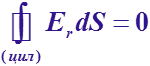Если r<R, то по теореме Гаусса

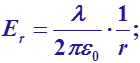
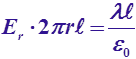
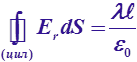                                и, E = 0

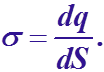
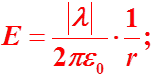 Если r>R, то        по т. Гаусса                                или                              те

 

 

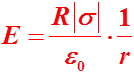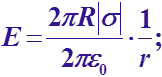тогда

Поле двух коаксиальных заряженных цилиндров

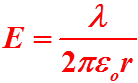
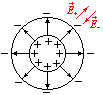Между цилиндрами поле определяется выражением 

Вне большого цилиндра вектора    Е+  и     Е-   направлены в разные стороны, и результирующее поле

Поле равномерно заряженной сферы

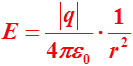
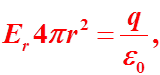
 Если                   то замкнутая поверхность не содержит внутри зарядов, поэтому в этой области всюду                Если                тогда по теореме Гаусса                                     тогда

3.  Работа перемещения заряда в электростатическом поле. Потенциал эл-стат. поля. Потенциал поля, создаваемого системой точечных зарядов. Энергия взаимодействия системы точечных зарядов.

В потенциальном поле работа по перемещению заряда не зависит от выбора траектории движения, а зависит лишь от начального и конечного положений заряда в этом поле. В этом случае работа по перемещению заряда по замкнутой траектории будет равна нулю