Оптическая корреляционная обработка, когерентно-оптический согласованный фильтр, страница 2

Предположим теперь, что входной световой поток однороден по амплитуде и фазе. Тогда световой поток справа от транспаранта модулируется только функцией S (х). Так как этот поток параллель­ный, то он сходится в точку в задней фокальной плоскости линзы, напряженность поля в которой равна интегралу от функции S (х).  Так выполняется операция интегрирования функции.

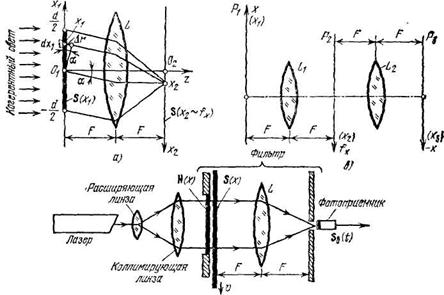
Рисунок 1.

Поскольку каждая точка транспаранта является источником колебаний, распространяющихся во всех направлениях, рассмотрим суммарный световой поток от всего транспаранта S (х₁) в произволь­ном направлении а α« π/2. При этом воспользуемся правилом, что луч, исходящий из главного фокуса (точка О₁), после линзы идет параллельно ее оси, а все параллельные лучи на входе линзы схо­дятся в одной точке х₂ задней фокальной плоскости. Если фазу сигнала, приходящего в точку х₂из точки О₁ принять равной нулю, то из-за разности хода Δr = x₁ sin α ≈ xα фаза сигнала, прихо­дящего из произвольной точки х₁ транспаранта, равна —2πfΔr/с  = =- 2nf_ox₁α/c. Ввиду этого напряженность поля, наводимого в точке х₂ элементом dx₁ транспаранта, можно характеризовать комплексной огибающей

S(x)exp(-j2πfxα/c)dx,

А напряжённость поля, создаваемого в этой точке всем транспарантом, определяется интегралом

S(α)=                     (1)

Введём пространственную частоту

f≈α/λ≈x/λF,                                   (2)