![]() ,
,
![]() ,
,
![]() ,
,
![]()
Сделаем расчет уравновешивающей силы:
![]()
![]()
Тогда уравновешивающий момент пары сил будет равен:
![]()
Задание 2.
Значения и направления внешних силовых факторов, действующих на звенья механизма, т. е. сил тяжести, мы нашли при выполнении первого задания. Составим расчетную модель механизма. Используя энергетический метод обеспечения эквивалентности динамической модели, построим динамическую модель механизма пригодную для выполнения динамического анализа, заменив все силовые факторы, действующие на ведомые звенья механизма, на приведенную силу.
Построим повернутый на 90º по ходу движения кривошипа план скоростей. На данный план перенесем вектора сил тяжести, действующие на звенья, в соответствующие точки и в том направлении, в котором они действуют.
По методу
Жуковского, сумма моментов вех сил ![]() , относительно полюса плана скоростей p, равна нулю:
, относительно полюса плана скоростей p, равна нулю:
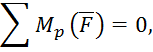
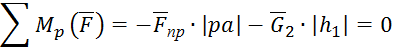
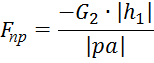
Измерим плечи сил на плане:
![]() ,
,
![]()
Сделаем расчет приведенной силы:
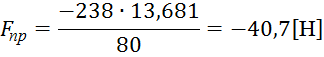
Тогда приведенный момент пары внешних сил будет равен:
![]()
В обоих случаях знак «–» говорит
о том, что приведенная сила ![]() и приведенный момент пары внешних сил
и приведенный момент пары внешних сил ![]() направлены в противоположную сторону движения
кривошипа.
направлены в противоположную сторону движения
кривошипа.
Значение приведенной массы технической системы вычислим по следующей формуле:
![]()
где ![]() постоянная и переменная части приведенной массы.
постоянная и переменная части приведенной массы.
Постоянная часть приведенной массы:
![]()
здесь ![]() приведенные массы соответственно энергетической
машины, преобразующего устройства и ведущего звена плоского рычажного механизма
рабочей машины.
приведенные массы соответственно энергетической
машины, преобразующего устройства и ведущего звена плоского рычажного механизма
рабочей машины.
Так как условиями лабораторной работы величины приведенных масс энергетической машины и преобразующего устройства не заданы, следовательно, значения этих параметров приравниваем к нулю:
![]() ,
,
![]() .
.
Переменная часть приведенной массы:
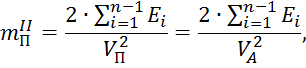
где ![]() линейная скорость звена приведения,
линейная скорость звена приведения, ![]() сумма кинетических энергий развиваемых приводимыми
звеньями механизма, n– количество подвижных звеньев
механизма.
сумма кинетических энергий развиваемых приводимыми
звеньями механизма, n– количество подвижных звеньев
механизма.
Сумма кинетических энергий развиваемых приводимыми звеньями кривошипно– ползунного механизма:
![]() .
.
Кинетическая энергия каждого приводимого звена:
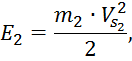
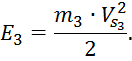
где:
![]()
![]()
![]()
Подставим полученные выражения в формулу переменной части приведенной массы:
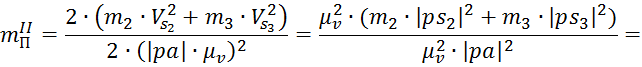
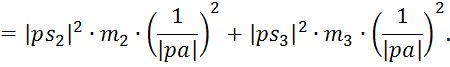
В полученную формулу подставим числовые данные:
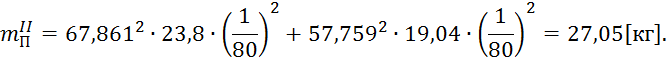
Приведенная масса технической системы будет равна:
![]()
Приведенный момент инерции вычислим по формуле:
![]()
![]()
Задание 3.
Обе динамические модели составляются с помощью метода приведения, который позволяет задачу о движении системы звеньев свести к более простой задаче о движении одного звена и подвижной точки этого звена. Данное звено, у обеих динамических моделей, называется звено приведения, а его подвижная точка- точка приведения. В обоих случаях в качестве звена приведения выбран кривошип 1, а за точку приведения принята точка А. Но динамическая модель для силового анализа составляется с использованием кинетостатического метода, согласно которого для сохранения эквивалентности модели по отношению к состоянию технической системы достаточно учесть только внешние и теоретические силовые факторы, т. е. силы тяжести, силы инерции и моменты пар сил инерции. При этом все силовые факторы, действующие на подвижные звенья технической системы, заменяются одной уравновешивающей силой. Вектор уравновешивающей силы прикладывается к точке приведения, а линия его действия является перпендикуляром к прямой ОА и вектор этой силы направлен по ходу движения кривошипа. Из-за наличия уравновешивающей силы на кривошипе появляется уравновешивающий момент.
Динамическая же модель, для динамического анализа, составляется с использованием энергетического метода, согласно которого для сохранения эквивалентности модели по отношению к состоянию технической системы необходимо учесть только внешние силовые факторы, т. е. силы тяжести. При этом все силовые факторы, действующие на ведомые звенья технической системы, заменяются одной силой, которая называется приведенной. Ее вектор прикладывается к точке приведения, направлен против движения кривошипа, а линия его действия является перпендикуляром к прямой ОА. Наличие приведенной силы на кривошипе является причиной появления приведенного момента пары сил. Также к точке приведения прикладывается теоретическая масса- масса приведения, состоящая из постоянной и переменной частей. Это является причиной появления приведенного момента инерции.
Вывод: хотя динамические модели технических систем и составляются с помощью одного общего метода приведения, но для разных видов их исследования следует учитывать отличительные признаки этих моделей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.